In an examination, six subjects - S1, S2, S3, S4, S5, and S6 have equal maximum marks. The number
of marks scored by one particular candidate in subject S1 is 20% less than his marks in subject S6. The
ratio of marks scored by the same candidate in subject S2 to that in S3 is 4: 5 and that in S4 to S5 is 3: 4. The
number of marks scored by this candidate in subject S5 is 25% more than that of S6. He scored 65 marks in the
subject S3. He scored 436/9 % in the examination and the average of marks scored by him in all the subjects is
218/3
What was the average of marks obtained by the candidate in the subject S5 and S6 together?
90
80
70
60
To solve the problem step by step, we will denote the marks scored by the candidate in each subject using variables based on the information provided.
Step 1: Define the marks in S6
Let the marks scored in subject S6 be 10x.
Step 2: Calculate the marks in S1
Since the marks in S1 are 20% less than in S6:
Marks in S1=10x−0.2×10x=10x×0.8=8x
Step 3: Calculate the marks in S3
We are given that the candidate scored 65 marks in subject S3.
Step 4: Calculate the marks in S2
The ratio of marks in S2 to S3 is 4:5. Therefore, if S3 = 65, we can find S2:
S2S3=45⟹S2=45×65=52
Step 5: Calculate the marks in S5
The marks in S5 are 25% more than in S6:
Marks in S5=10x+0.25×10x=10x×1.25=12.5x
Step 6: Calculate the marks in S4
The ratio of marks in S4 to S5 is 3:4. Therefore:
S4S5=34⟹S4=34×12.5x=37.5x4=9.375x
Step 7: Set up the total marks equation
The average marks scored by the candidate in all subjects is 2183. Since there are 6 subjects, the total marks will be:
Total Marks=6×2183=436
Step 8: Write the equation for total marks
Now, we can write the equation for total marks:
8x+52+65+9.375x+12.5x+10x=436
Step 9: Combine like terms
Combining the terms:
(8x+9.375x+12.5x+10x)+(52+65)=436
39.875x+117=436
Step 10: Solve for x
Subtract 117 from both sides:
39.875x=319
Now divide by 39.875:
x=31939.875≈8
Step 11: Calculate marks in S5 and S6
Now we can calculate the marks in S5 and S6:
- Marks in S6:
S6=10x=10×8=80
- Marks in S5:
S5=12.5x=12.5×8=100
Step 12: Calculate the average of marks in S5 and S6
The average of marks in S5 and S6 together:
Average=S5+S62=100+802=1802=90
Final Answer
The average of marks obtained by the candidate in the subjects S5 and S6 together is 90.
---
Let the marks scored in subject S6 be 10x.
Since the marks in S1 are 20% less than in S6:
Marks in S1=10x−0.2×10x=10x×0.8=8x
We are given that the candidate scored 65 marks in subject S3.
The ratio of marks in S2 to S3 is 4:5. Therefore, if S3 = 65, we can find S2:
S2S3=45⟹S2=45×65=52
The marks in S5 are 25% more than in S6:
Marks in S5=10x+0.25×10x=10x×1.25=12.5x
The ratio of marks in S4 to S5 is 3:4. Therefore:
S4S5=34⟹S4=34×12.5x=37.5x4=9.375x
The average marks scored by the candidate in all subjects is 2183. Since there are 6 subjects, the total marks will be:
Total Marks=6×2183=436
Now, we can write the equation for total marks:
8x+52+65+9.375x+12.5x+10x=436
Combining the terms:
(8x+9.375x+12.5x+10x)+(52+65)=436
39.875x+117=436
Subtract 117 from both sides:
39.875x=319
Now divide by 39.875:
x=31939.875≈8
Now we can calculate the marks in S5 and S6:
- Marks in S6:
S6=10x=10×8=80
- Marks in S5:
S5=12.5x=12.5×8=100
The average of marks in S5 and S6 together:
Average=S5+S62=100+802=1802=90
The average of marks obtained by the candidate in the subjects S5 and S6 together is 90.
Similar Questions
In an examination, six subjects - S1, S2, S3, S4, S5, and S6 have equal maximum marks. The number of marks scored by one particular candidate in subject S1 is 20% less than his marks in subject S6. The ratio of marks scored by the same candidate in subject S2 to that in S3 is 4: 5 and that in S4 to S5 is 3: 4. The number of marks scored by this candidate in subject S5 is 25% more than that of S6. He scored 65 marks in the subject S3. He scored 436/9 % in the examination and the average of marks scored by him in all the subjects is 218/3
The number of marks obtained by the candidate in the subject S3 was how much percentage less than that of subject S5?
View SolutionIn an examination, six subjects - S1, S2, S3, S4, S5, and S6 have equal maximum marks. The number of marks scored by one particular candidate in subject S1 is 20% less than his marks in subject S6. The ratio of marks scored by the same candidate in subject S2 to that in S3 is 4: 5 and that in S4 to S5 is 3: 4. The number of marks scored by this candidate in subject S5 is 25% more than that of S6. He scored 65 marks in the subject S3. He scored 436/9 % in the examination and the average of marks scored by him in all the subjects is 218/3
The number of marks obtained by the candidate in the subject S2 was how much less than in the subject S4?
View Solution
Knowledge Check
Highest marks are scored in the subject
AEnglishBHindiCMathsDNone of theseThe marks obtained in 4 subjects in an examination are 200. If the average of marks obtained in 3 subjects is 48, then how many marks are obtained in fourth subject?
A50B144C152D56
In an examination, six subjects - S1, S2, S3, S4, S5, and S6 have equal maximum marks. The number of marks scored by one particular candidate in subject S1 is 20% less than his marks in subject S6. The ratio of marks scored by the same candidate in subject S2 to that in S3 is 4: 5 and that in S4 to S5 is 3: 4. The number of marks scored by this candidate in subject S5 is 25% more than that of S6. He scored 65 marks in the subject S3. He scored 436/9 % in the examination and the average of marks scored by him in all the subjects is 218/3
What percentage of marks the candidate had scored in the subject S5 over the maximum marks of that subject?
View SolutionIn an examination, six subjects - S1, S2, S3, S4, S5, and S6 have equal maximum marks. The number of marks scored by one particular candidate in subject S1 is 20% less than his marks in subject S6. The ratio of marks scored by the same candidate in subject S2 to that in S3 is 4: 5 and that in S4 to S5 is 3: 4. The number of marks scored by this candidate in subject S5 is 25% more than that of S6. He scored 65 marks in the subject S3. He scored 436/9 % in the examination and the average of marks scored by him in all the subjects is 218/3
Total marks scored by S2 and S3 is multiple of which of the following pairs.
View SolutionA student scores 65, 62 70 marks is 3 subjects. Find the minimum marks scored by him in 4th subject to get an average of 64 minimun.
View SolutionThe table given below shows the marks obtained by 6 students in 3 subjects.
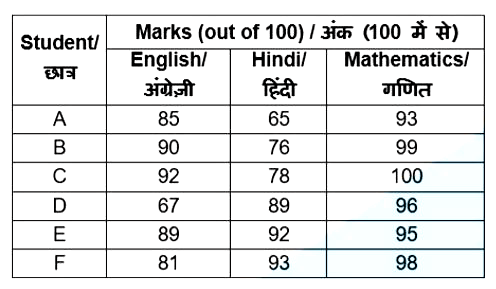
What are the average marks per subject scored by D?
View SolutionThe pie chart given shows the number of marks scored by a student in the given 5 subjects. The total marks scored by the student is 480.
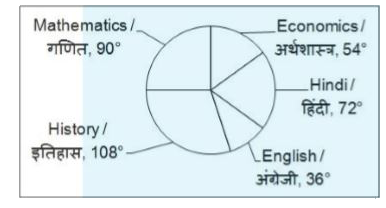
What is the average marks scored by the student in Hindi and Mathematics?
View SolutionThe pie chart given shows the number of marks scored by a student in the given 5 subjects. The total marks scored by the student is 480.
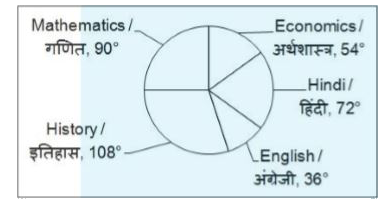
The marks scored by the student in Hindi is how much percent more than the marks scored in Economics?
View Solution