Question

A particle is projected from a towaer as shown in figure, then the distance from the foot of the tower where it will strike the ground will be :- $(\text{take}g=10m/s^2)$

Explanation

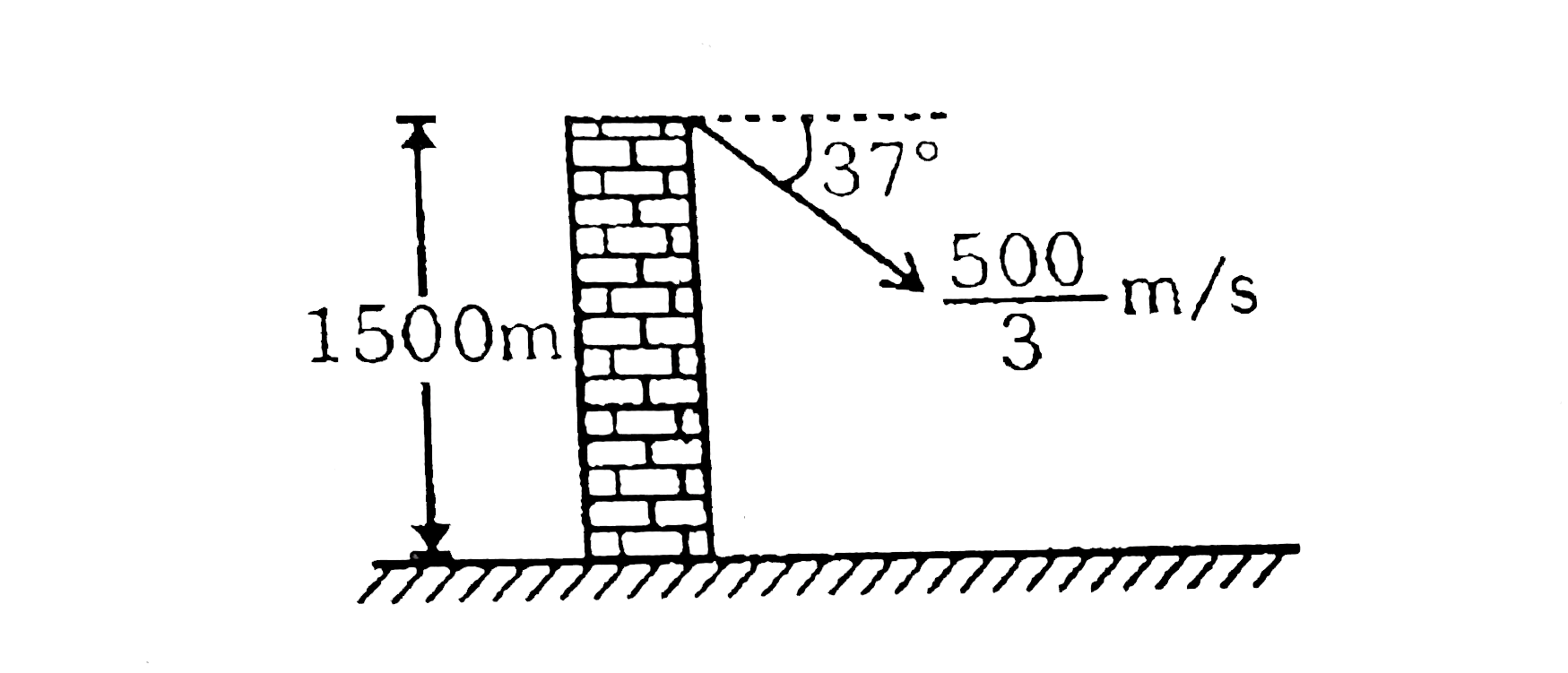
`s = ut+(1)/(2) at^(2)`
`1500 = (1500)/(3)sin 37 + (1)/(2)10xxt^(2)`

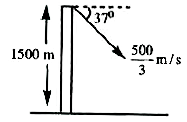
`1500 = (500)/(3)xx(3)/(5)t+5t^(2) rArr 300 = 20t + t^(2)`
On solving, t =10s
`:. "Horizontal distance" = u costheta.T`
`=(500)/(3)xx(4)/(5)xx10=(4000)/(3)m`.