Vector →A is 2 cm long and is 60° above the x - axis in the first quadrant, vector →B is 2cm long and is 60° below the x - axis in the fourth quadrant. Find →A+→B
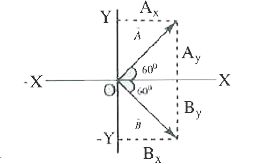
→R=→A+→B
→R=2cos600ˆi+2sin60ˆj+2cos60ˆi−2sin60ˆj
→R=4cos60ˆi=2ˆi
:.2cm, along x-axis
Similar Questions
Vector →A is 2cm long and is 60∘ above the x-axis in the first quadrant. Vactor →B is 2cm long and is 60∘ below the x-axis in the fourth quadrant. The sum →A+→B is a vector of magnitudes
View Solution→Aand→B are two vectors such that →A is 2 m long and is 60∘ above the x - axis in the first quadrant →B is 2 m long and is 60∘ below the x - axis in the fourth quadrant .
Draw diagram to show →a+→B,→A−→Band→B−→A
(b) What is the magnitude and direction of →A+→B,→A−→Band→B−→A
View SolutionA vector →A is along the positive z-axis and its vector product with another vector →B is zero, then vector →B could be :
View SolutionIf →A+→B is a unit vector along x-axis and →A=ˆi−ˆj+ˆk, then what is →B ?
View SolutionIf →A+→B is a unit vector along x-axis and →A=ˆi−ˆj+ˆk, then what is →B?
View SolutionIf the angle between unit vectors →aand→bis60∘ . Then find the value of ∣∣→a−→b∣∣.
View SolutionIf the angle between unit vectors →aand→bis60∘ . Then find the value of ∣∣→a−→b∣∣.
View Solutionif →a,→band→c are there mutually perpendicular unit vectors and →a ia a unit vector then find the value of ∣∣2→a+→b+→c∣∣2
View SolutionFind the angle between unit vector →a and →b so that √3 →a - →b is also a unit vector.
View SolutionFind the angle between unit vector →a and →b so that √3 →a - →b is also a unit vector.
View Solution
