Vector →A is 2cm long and is 60∘ above the x-axis in the first quadrant. Vactor →B is 2cm long and is 60∘ below the x-axis in the fourth quadrant. The sum →A+→B is a vector of magnitudes
2cm along positive y-axis
2cm along positive x-axis
2cm along negative y-axis
2cm along negative x-axis
The correct Answer is:B
To solve the problem of finding the magnitude of the resultant vector →R=→A+→B, we will follow these steps:
Step 1: Determine the components of vector →A
Vector →A has a magnitude of 2cm and is directed 60∘ above the x-axis. We can find its components using trigonometry:
- Ax=Acos(60∘)=2cos(60∘)=2×12=1cm
- Ay=Asin(60∘)=2sin(60∘)=2×√32=√3cm
Step 2: Determine the components of vector →B
Vector →B has a magnitude of 2cm and is directed 60∘ below the x-axis. Its components are:
- Bx=Bcos(60∘)=2cos(60∘)=2×12=1cm
- By=Bsin(−60∘)=2sin(−60∘)=2×−√32=−√3cm
Step 3: Find the resultant components
Now, we can find the components of the resultant vector →R:
- Rx=Ax+Bx=1+1=2cm
- Ry=Ay+By=√3+(−√3)=0cm
Step 4: Calculate the magnitude of the resultant vector
The magnitude of the resultant vector →R is given by:
|→R|=√R2x+R2y=√(2)2+(0)2=√4=2cm
Step 5: Determine the direction of the resultant vector
Since Ry=0 and Rx=2cm, the resultant vector →R is directed along the positive x-axis.
Final Answer
The magnitude of the resultant vector →R is 2cm and it is directed along the positive x-axis.
---
Vector →A has a magnitude of 2cm and is directed 60∘ above the x-axis. We can find its components using trigonometry:
- Ax=Acos(60∘)=2cos(60∘)=2×12=1cm
- Ay=Asin(60∘)=2sin(60∘)=2×√32=√3cm
Vector →B has a magnitude of 2cm and is directed 60∘ below the x-axis. Its components are:
- Bx=Bcos(60∘)=2cos(60∘)=2×12=1cm
- By=Bsin(−60∘)=2sin(−60∘)=2×−√32=−√3cm
Now, we can find the components of the resultant vector →R:
- Rx=Ax+Bx=1+1=2cm
- Ry=Ay+By=√3+(−√3)=0cm
The magnitude of the resultant vector →R is given by:
|→R|=√R2x+R2y=√(2)2+(0)2=√4=2cm
Since Ry=0 and Rx=2cm, the resultant vector →R is directed along the positive x-axis.
The magnitude of the resultant vector →R is 2cm and it is directed along the positive x-axis.
Topper's Solved these Questions
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Subjective
28 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Integer
9 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (integer)
4 Videos
Similar Questions
Vector →A is 2 cm long and is 60° above the x - axis in the first quadrant, vector →B is 2cm long and is 60° below the x - axis in the fourth quadrant. Find →A+→B
View Solution→Aand→B are two vectors such that →A is 2 m long and is 60∘ above the x - axis in the first quadrant →B is 2 m long and is 60∘ below the x - axis in the fourth quadrant .
Draw diagram to show →a+→B,→A−→Band→B−→A
(b) What is the magnitude and direction of →A+→B,→A−→Band→B−→A
View SolutionA vector →B which has a magnitude 8.0 is added to a vector →A which lies along the x-axis. The sum of these two vector is a third vector which lies along the y-axis and has a magnitude that is twice the magnitude of →A. Find the magnitude of →A
View SolutionA vector →A of length 10 units makes an angle of 60∘ with a vector →B of length 6 units. Find the magnitude of the vector difference →A−→B & the angles with vector →A.
View SolutionLet −−→AB be a vector in two dimensional plane with magnitude 4 units. And making an anle of 600 with x-axis, and lying in first quadrant. Find the components of −−→AB in terms of unit vectors ˆiandˆj. so verify that calculation of components is correct.
View SolutionFind the magnitude of the sum of →Aand→B and its direction with respect to the X - axis .
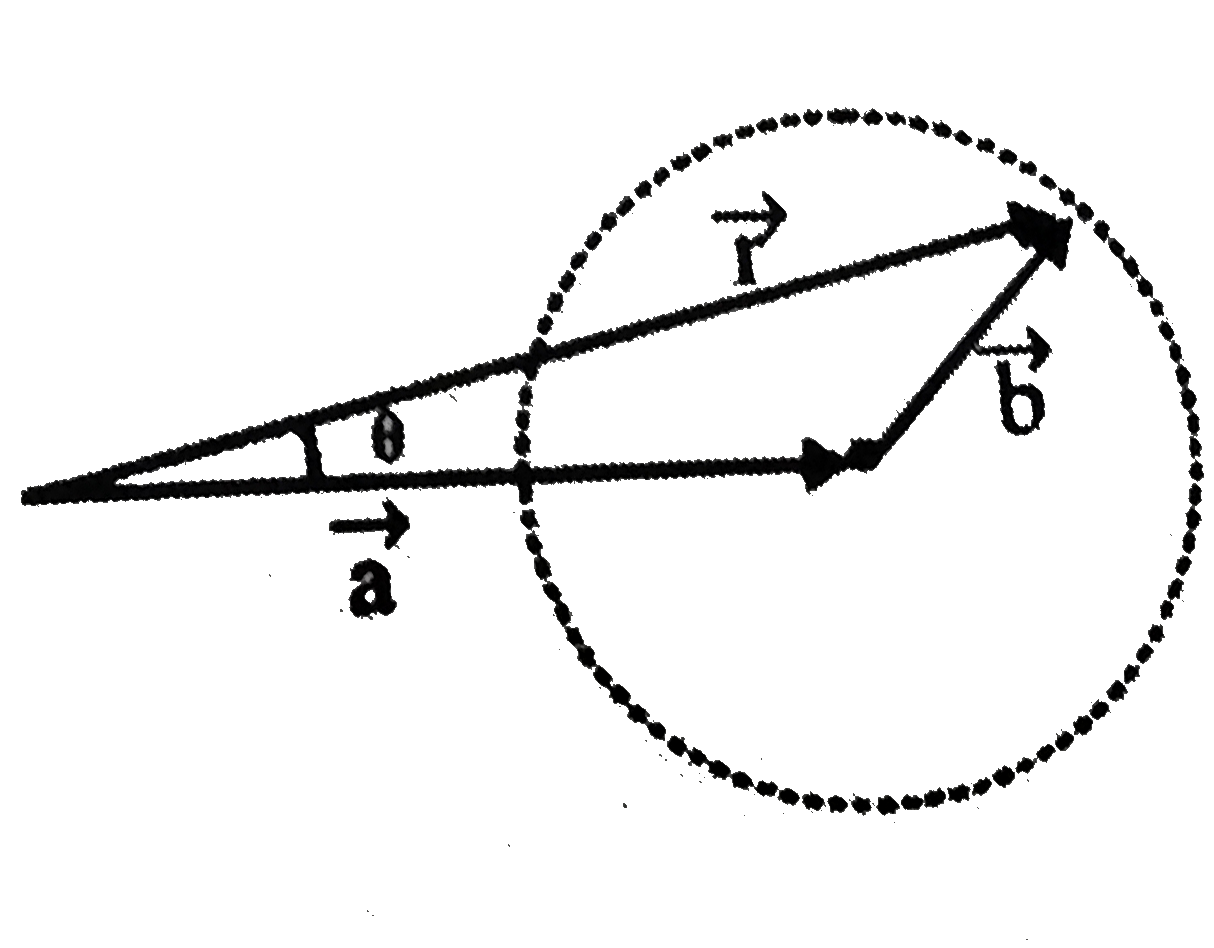
View SolutionKeeping one vector constant, if direction of other to be added in the first vector is changed continuously, tip of the resultant vector describes a circles, In the following figure vector →a is kept constant. When vector →b addede to →a changes its direction, the tip of the resultant vector →r=→a+→b describes circles of radius b with its centre at the tip of vector →a. Maximum angle between vector →a and the resultant →r=→a+→b is
View Solution→Aand→B are two vectors having the same magnitude . What is the condition that (i) the vector sum →A+→B and (ii) the vector differece →A+→B have the same magnitude as →Aand→B ?
View SolutionThe angle between vectors →Aand→B is 60∘ What is the ratio →A.→B and ∣∣→A×→B∣∣
View SolutionIf for two vectors ˆA and ˆB,sum (→A+→B) is perpendicular to the diffrence (→A−→B). Find the ratio of their magnitude.
View Solution
