Check the correctness of the formula S=ut+13at2 where S is the distance , u is velocity , a is acceleration and t is time.
Dimensionally, LHS=[L]
RHS=[LT−1][T]+[LT−2][T]2=[L]+[L]
Since, the dimension of each term on both sides are same, the equation is correct dimensionally, However, we cannot say anything about the physical correctness of the formula . in fact, we know that the correct formula is S=ut+12at2
Hence, we conslude that dimensional correctness is no guarantee for physical correctness of the formula. however, dimensional incorrectness guarantees the physical incorrectness of the fomula. Inspite to the above limitation, the method is still helpful to a great extent.
Similar Questions
Chek the correctness of the relation, Snth=u+a2(2n−1), where u is initial velocity, a is acceleratin and Snth is the distance travelled by the body in nth second.
View SolutionCheck the correctness of following equation by the method of dimensions :
S=ut+12at2 .
where S is the distance covered bu a body in time t, having initial velocity u and acceleration a.
View SolutionCheck the correctness of the equations (i) s=ut+12at2 (ii) v2=u2+2as using dimensions.
View SolutionA particle starts rotating from rest according to the formula θ=(t2/64)−(t/8) where θ is the angle in radian and t in s . Find the angular velocity and angular acceleration at the end of 4 s .
View SolutionThe motion of a particle along a straight line is described by the function x=(2t−3)2, where x is in metres and t is in seconds. Find
(a) the position, velocity and acceleration at t=2s.
(b) the velocity of the particle at origin.
View SolutionThe motion of a particle along a straight line is described by the function x=(2t−3)2, where x is in metres and t is in seconds. Find
(a) the position, velocity and acceleration at t=2s.
(b) the velocity of the particle at origin.
View Solution(a) Write a equation of motion in different states and derive the relation :
s=u+12a(2t−1)
Where, s is the distance covered in tth second, u is initial velocity and a is uniform acceleration.
View SolutionThe distance travelled by a particle in nth second is Sn=u+a2(2n−1) where u is the velocity and a is the acceleration. The equation is
View SolutionFigure is a graph of the coordinate of a spider crawling along the x-axis. (a) Fraph tis velocity and acceleration as functionsof time. (b) In a motion diagram, show the position, velocity, and acceleration of the spider at the five times: t=2.5s, t=10 s, t=20 s, t=30 s,
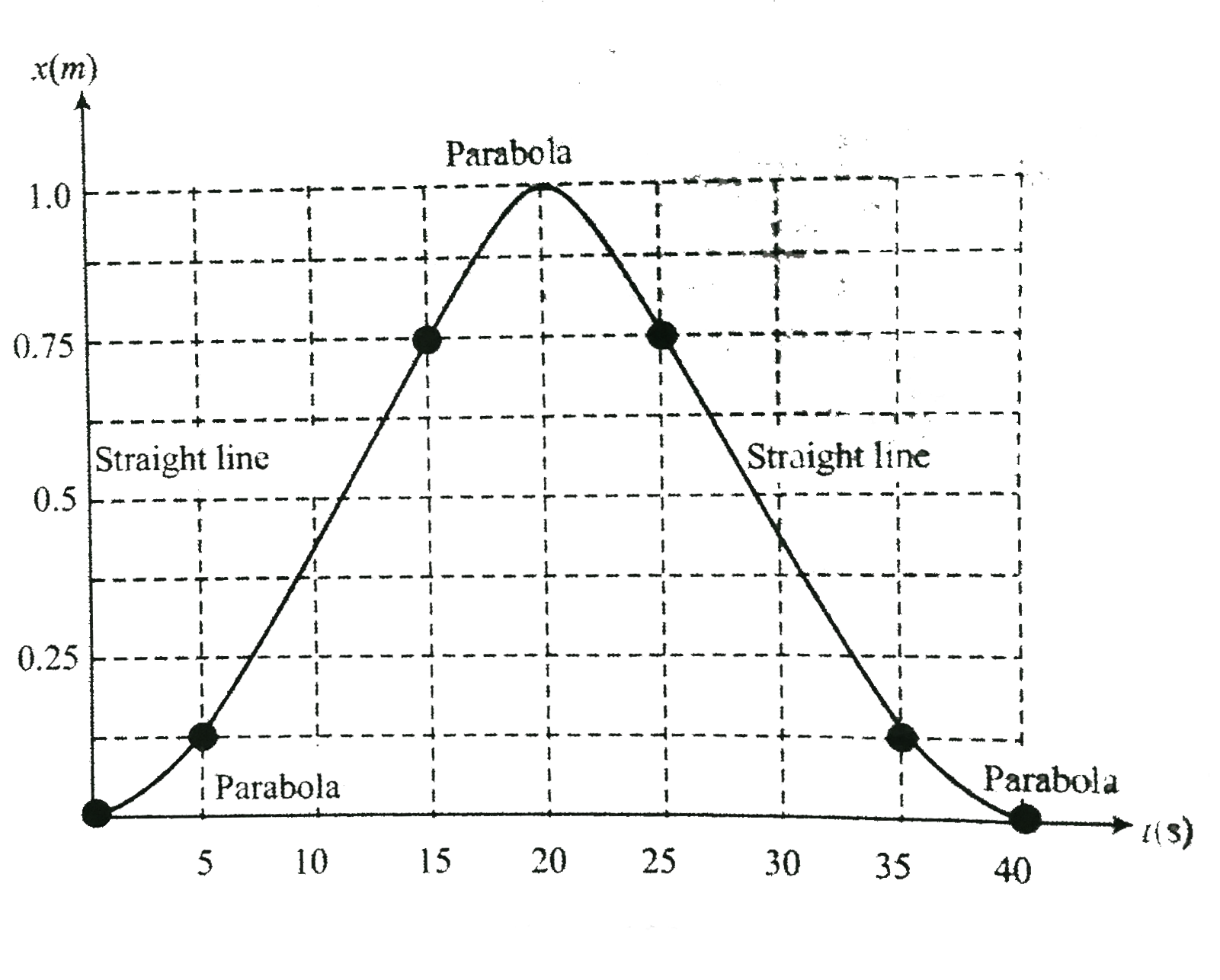 .
.
View SolutionA car is running on a straight road . The distance travelled and time taken are connected by the formula =t2−2t where t is measured in hours and s in km. When the odometer reading is 15, what is the speedometer reading ? [ Odometer measures s and the speedmeter measures velocity]
View Solution
