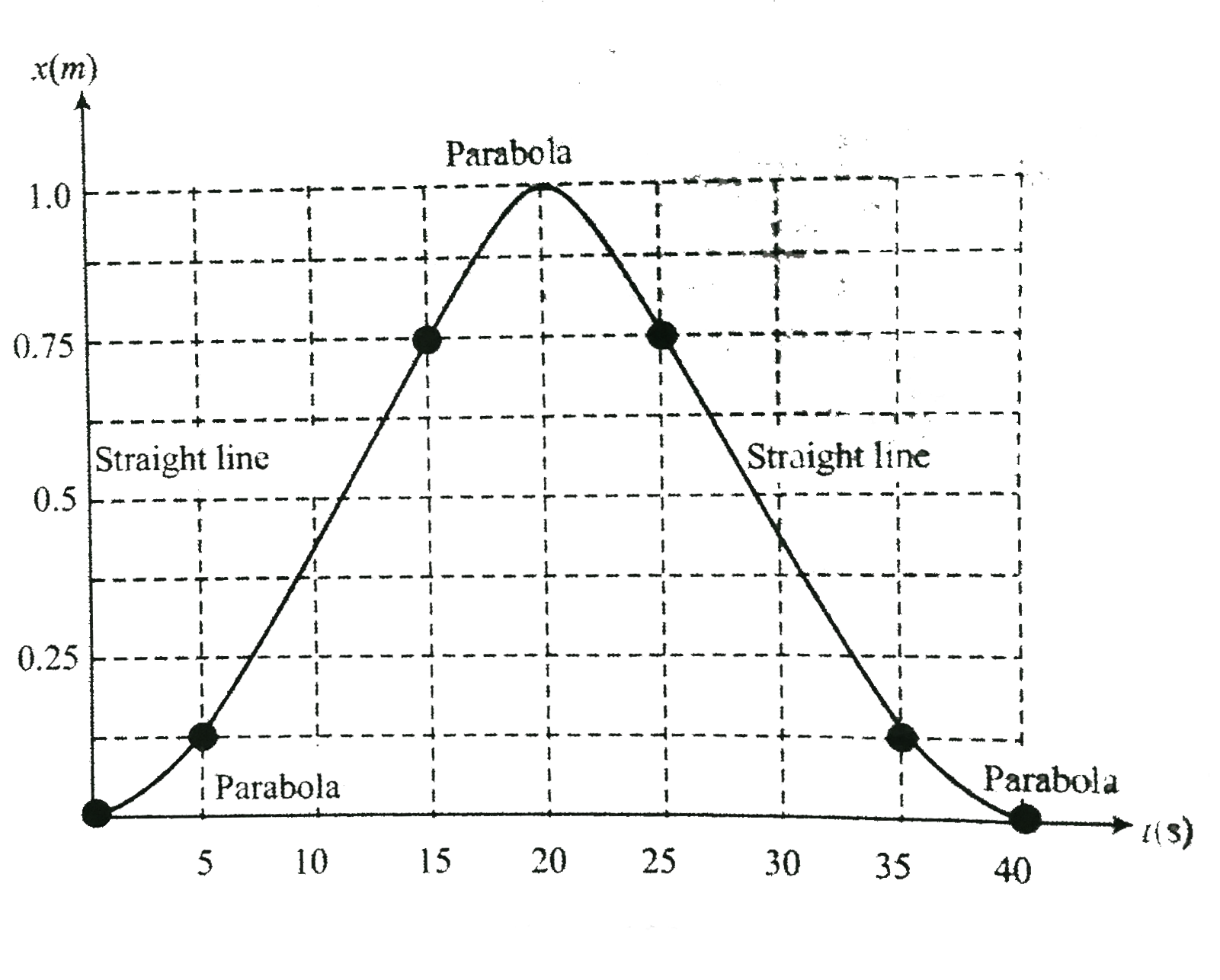
Figure is a graph of the coordinate of a spider crawling along the x-axis. (a) Fraph tis velocity and acceleration as functionsof time. (b) In a motion diagram, show the position, velocity, and acceleration of the spider at the five times: t=2.5s, t=10 s, t=20 s, t=30 s,
 .
.
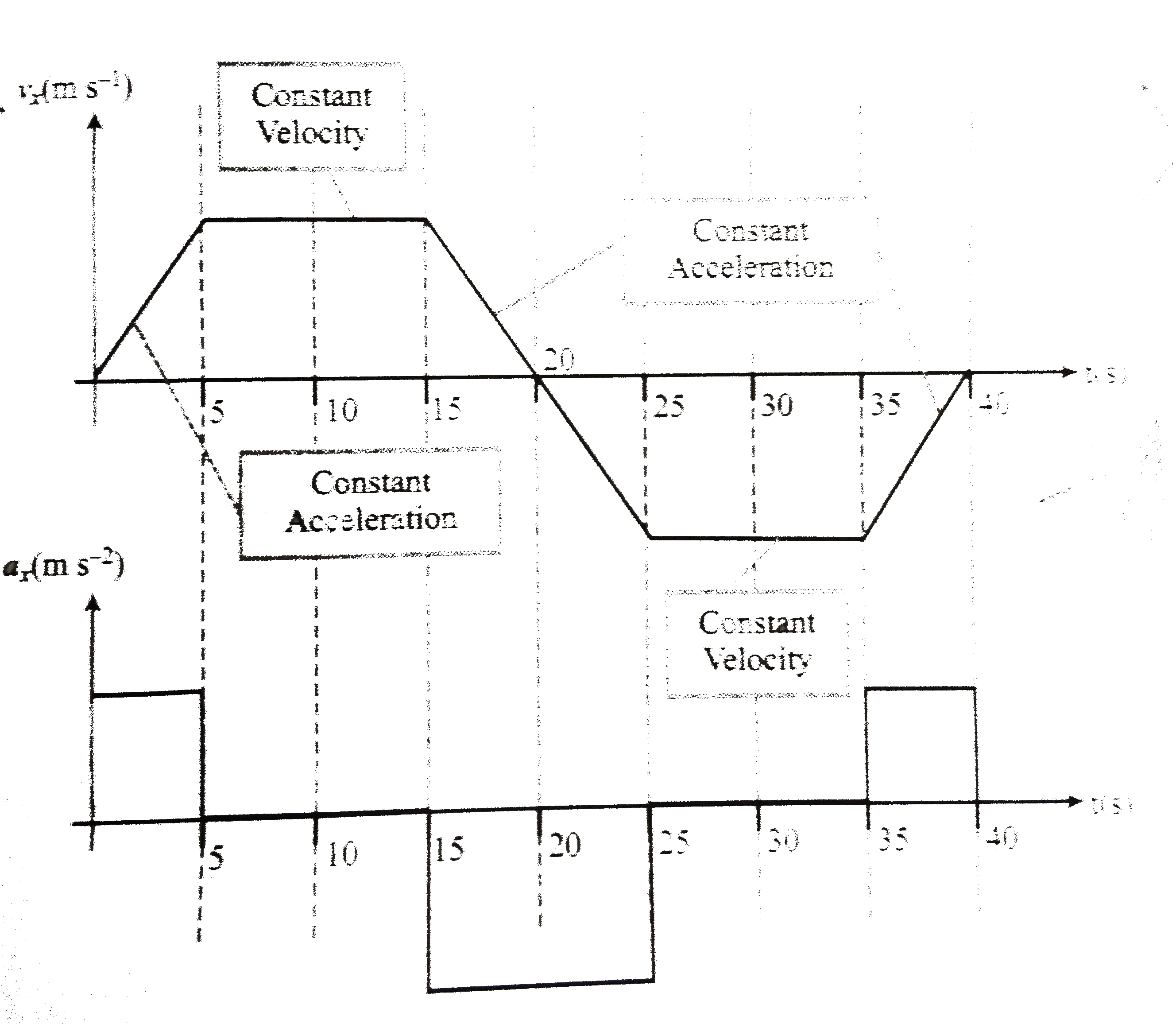
a. vx is the slope of the x versus t curve and ax is the slope of the vx versus t curve.
t=O to t=5s: x versus t is a parabola, so ax versus t is The curvature s positive so ax is positive vx versus t is a straight line with positive slope. vx=0.
t=5s to t=25s: x versus t is a straight line, so vx is constant and 0. ax=0. The slope of x versus t is positive, so vx is positive.
t=15s to t=25s: x versus t is a parabola with negative curvature, so ax is constant and negative, vx versus t is a straight line with negative slope. The velocity is zero at 20s, positive to 15s to 20s, and negative to 20s to 25s. t=25s to t=35s: x versus t is a straight line, so vx is constant and ax=0. The slope of x versus t is negative, so vx is negative.
t=35s to t=40s: x versus t is a parabola with positive curvature, so ax is constant and positive.
vx versus t is a straight line with positive slope. The velpcoty reaches zero at t=40s
The graphs of vx(t) are sketched in
 .
.
b. The motions diagrams are skerched in
 .
.
The spider speeds up for the first 5s, since vx and ax are both positive. Starting at t=5s, the spider starts to slow down stops momentarily at t=20s, and then moves in the opposite direction. At t=35s, the spider sarts in the opppsits direction .At t=35s, the spider starts to slow down again and stops at t=40.
Topper's Solved these Questions
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Solved Examples
9 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.1
17 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer
9 Videos
Similar Questions
The displacement of a particle along the x-axis is given by x=3+8t+7t2. Obtain its velocity and acceleration at t=2s.
View SolutionFig. shows the graph of the x-coordinate of a particle going along the x-axis as a function of time. Find (a) the average velocity during 0 to 10s, (b) instantaneous velocity at 2, 5, 8 and 12s.

View SolutionFigure shows the graph of the x-coordinaste of a particle going along the X-axis as a function of time.Find a. te average velocity during 0 to 10s, b. instantaneous velocity at 2,5,8 and 12s.

View SolutionConsiedr the following x−t garaph to be parabolic. Draw the velocity-time graph and acceleration-time graph analyze the motion of the particle regarding its velocity and acceleration.
 .
.
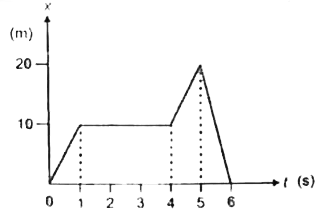
View SolutionFigure shows the graph of x - coordinate of a particle moving along x - axis as a function of time. Average velocity during t = 0 to 6 s and instantaneous velocity at t = 3 s respectively, will be
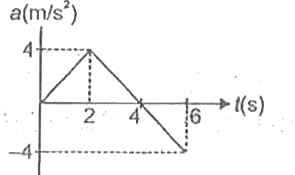
View SolutionFor the acceleration - time (a - t) graph shown in figure, the change in velocity of particle from t = 0 to t = 6 s is
View SolutionA particle starts from the origin at time t = 0 and moves along the positive x-axis. The graph of velocity with respect to time is shown in figure. What is the position of the particle at time t = 5s ?

View SolutionFigure shows the graph of x-coordinate of a particle moving along x-axis as a function of time. Average velocity during t = 0 to 4 s and instantaneous velocity at t = 4.113 s respectively will be

View SolutionThe x-t graph of a particle undergoing simple harmonic motion is shown below. The acceleration of the particle at t=23s is

View SolutionA particle starts to move in a straight line from a point with velocity 10 m s−1 and acceleration - 2.0 ms−2. Find the position and velocity of the particle at (i) t = 5 s, (ii) t' = 10 s.
View Solution
