A right body can be hinged about any point on the x-axis. When it is hinged such that the hinge is at x, the moment of inertia is given by
l=2x2−12x+27
The x-coordinate of centre of mass is
The correct Answer is:3
Step by step video solution for A right body can be hinged about any point on the x-axis. When it is hinged such that the hinge is at x, the moment of inertia is given by l=2x^(2)-12x+27 The x-coordinate of centre of mass is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
A rigid body can be hinged about any point on the x-axis. When it is hinged such that the hinge is at x, the moment of interia is given by
I=2x2−12x+27
The x-coordinate of centre of mass is.
View SolutionAny point on the X-axis is of the form
View SolutionA rod is placed along the line,y=2x with its centre at origin. The moment of inertia of the rod is maximum about.
View SolutionMoment of inertia of a disc about an axis parallel to diameter and at a distance x from the centre of the disc is same as the moment of inertia of the disc about its centre axis. The radius of disc is R. The value of x is
View SolutionThe figure shows an isosceles triangle plate of mass M and base L.
The angle at the apex is 90∘. The apex lies at the origin and the base is parallel to X−axis.

The moment of inertia of the plate about its base parallel to the x−axis is
View SolutionThe figure shows an isosceles triangle plate of mass M and base L.
The angle at the apex is 90∘. The apex lies at the origin and the base is parallel to X−axis.
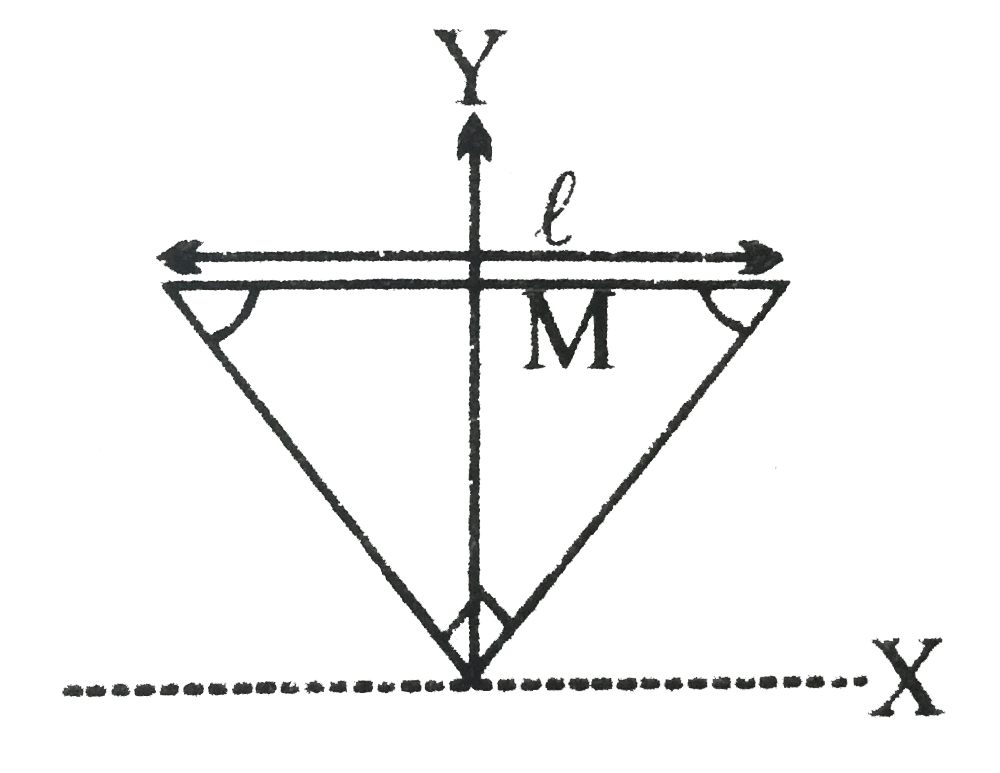
The moment of inertia of the plate about the y−axis is
View SolutionFind the points of local maxima and minima of the function f given by f(x)=x3−12x2+36x+5 .
View SolutionFind the equation of the curve passing through the point (0, -2) given that at any point (x,y) on the curve the product of the slope of its tangent and y coordinate of the point is equal to the x-coordinate of the point.
View SolutionThe tangent at any point P on y2=4x meets x-axis at Q, then locus of mid point of PQ will be
View SolutionWhen a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
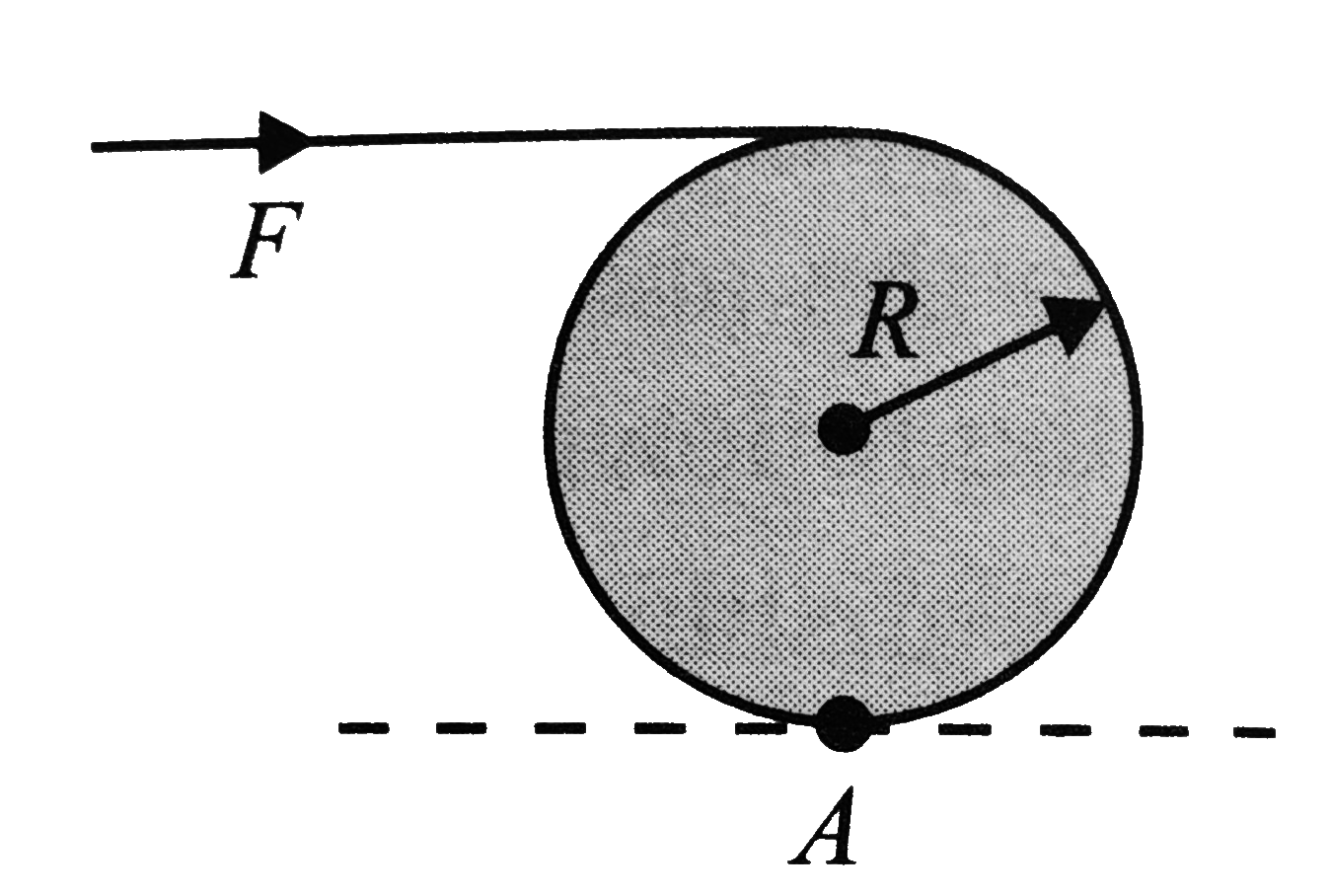
Tangential acceleration of the centre of mass is
View Solution
