When a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
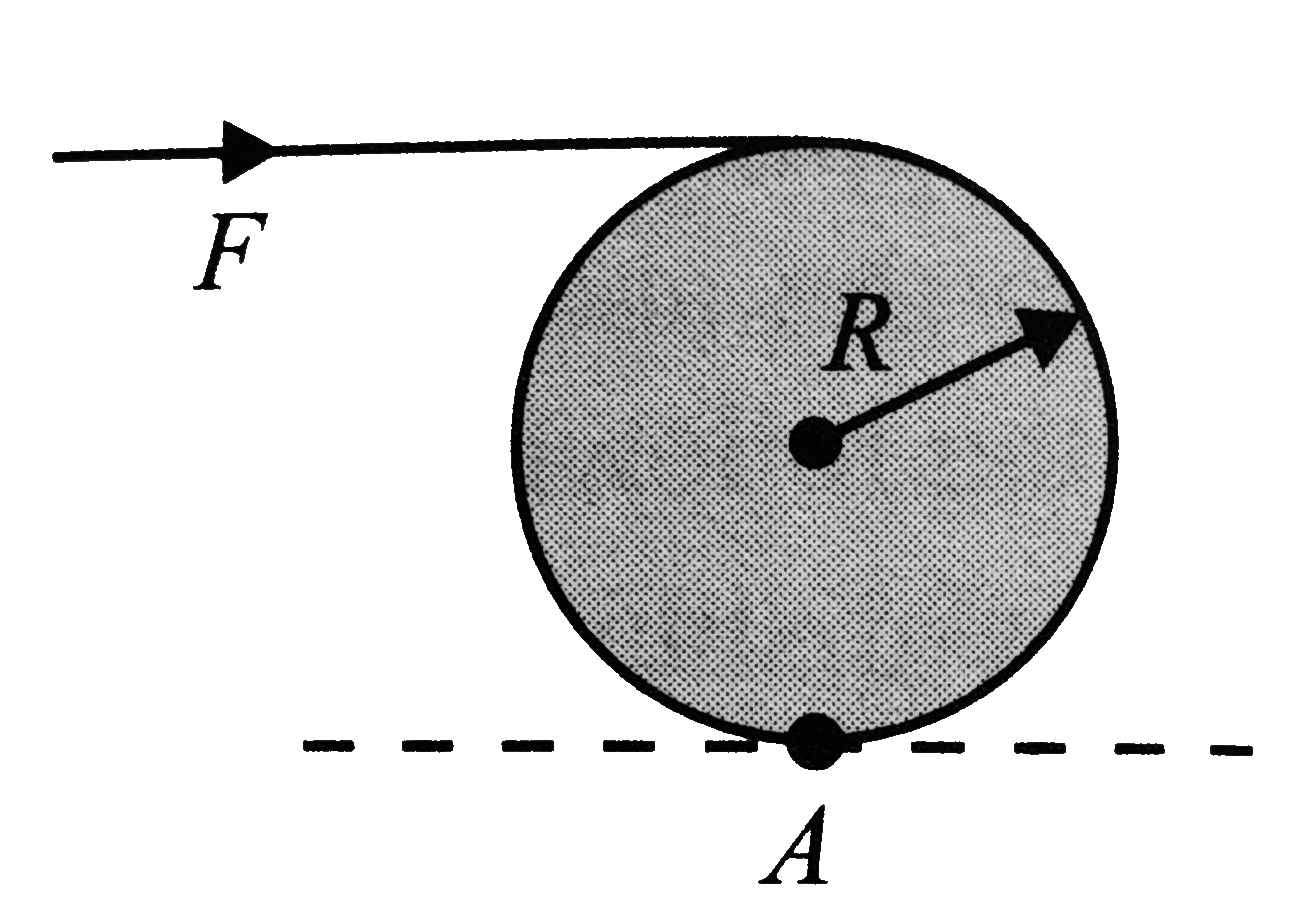
Component of reaction at the hinge in the horizontal direction is
F4
F
F3
F2
The correct Answer is:C
Torque about the CM
(F−Rx)R=Iα
⇒(F−Rx)R=Mr2at2r
⇒(F−Rx)R=2F3
⇒F=2F3=Rx⇒Rx=F3
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Integer
Explore 7 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Fill In The Blanks
Explore 7 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Multiple Correct
Explore 26 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICSChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Integer
Explore 16 Videos
Similar Questions
Knowledge Check
When a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
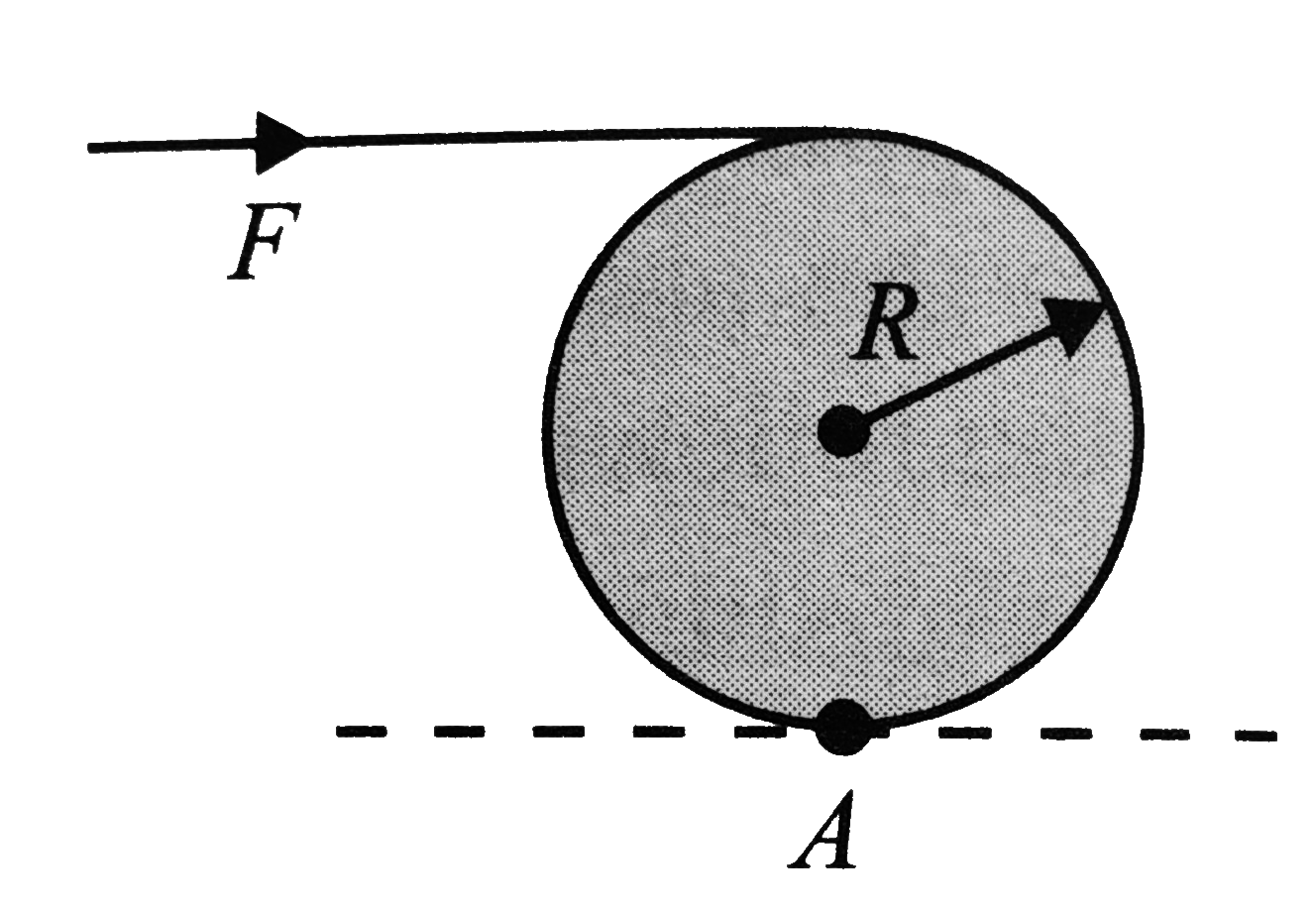
Component of reaction at the hinge in the vertical direction isA43mgBmgCMg2D23mgWhen a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
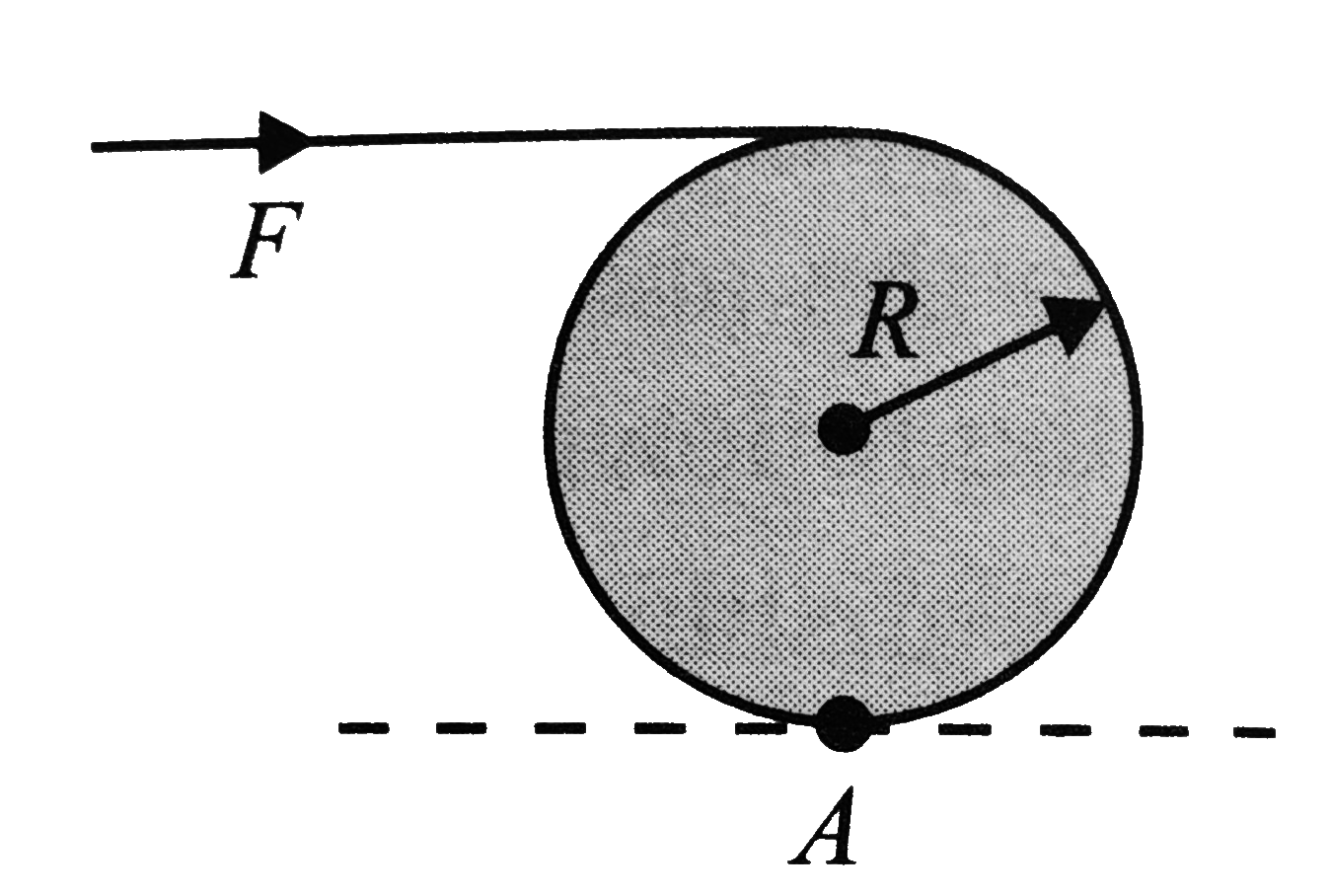
Tangential acceleration of the centre of mass isA3F4mBFmC2F3mD4F3mWhen a steady torque (net force is zero) is acting on a body, the body.
Arotates at a constant speedBgets both linear and angular accelerationCgets no angular accelerationDcentre of the body continues in its state of rest or uniform motion along a straight line.
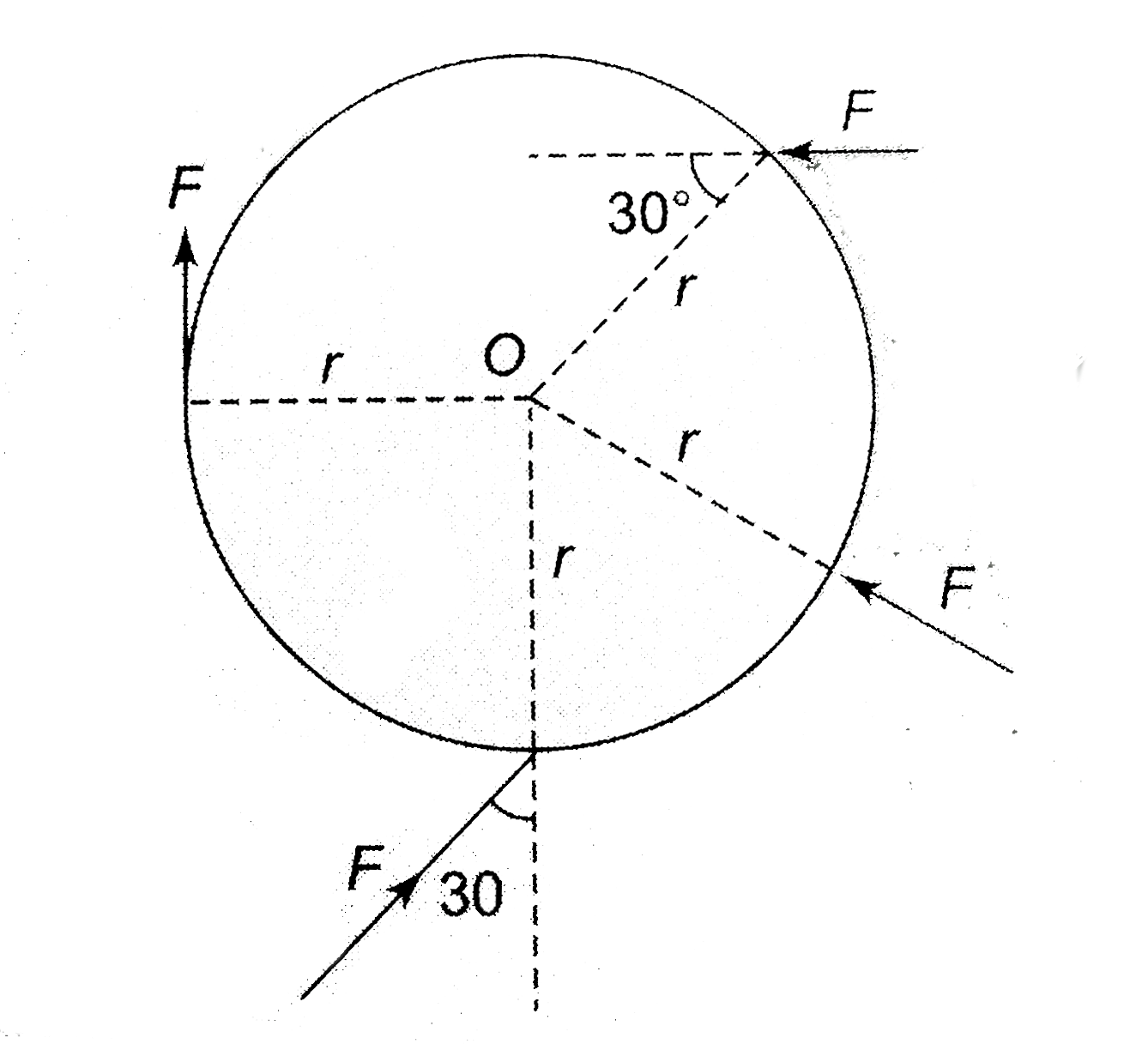
Calculate the total torque acting on the body shown in figure about the point O
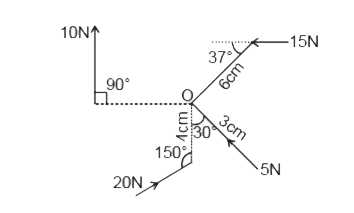
View SolutionFind the frequency of small oscillations of thin uniform vertical rod of mass m and length l hinged at the point O.

View SolutionCalculate the total torque acting on the body shown in figure about the point O.

View SolutionA uniform disc of mass M and radius R is hinged at its centre C. A force F is applied on the disc as shown. At this instant, the angular acceleration of the disc is
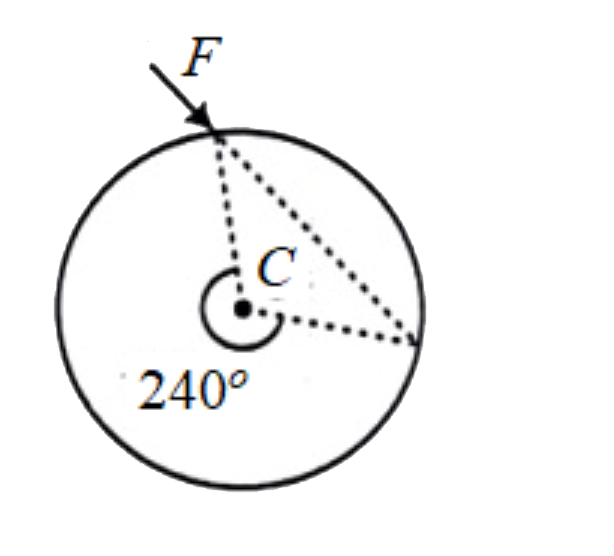
View SolutionA body is under the action of two equal and oppositely directed forces and the body is rotating with constant non-zero angular acceleration. Which of the following cannot be the separation between the lines of action of the forces ?
View Solution