Two particles each of the same mass move due north and due east respectively with the same velocity .V.. The magnitude and direction of the velocity of centre of mass is
V√2NE
√2VNE
2VSW
V2SW
The correct Answer is:A
To find the magnitude and direction of the velocity of the center of mass (COM) of two particles moving in perpendicular directions, we can follow these steps:
Step 1: Define the system
Let’s denote the two particles:
- Particle 1 is moving due north with velocity →v1=v^j (where ^j is the unit vector in the north direction).
- Particle 2 is moving due east with velocity →v2=v^i (where ^i is the unit vector in the east direction).
Step 2: Assign masses
Let both particles have the same mass m.
Step 3: Calculate the velocity of the center of mass
The velocity of the center of mass →Vcm is given by the formula:
→Vcm=m1→v1+m2→v2m1+m2
Since both particles have the same mass m:
→Vcm=m→v1+m→v2m+m=→v1+→v22
Substituting the velocities:
→Vcm=v^j+v^i2=v2^i+v2^j
Step 4: Find the magnitude of the center of mass velocity
To find the magnitude of →Vcm:
|→Vcm|=√(v2)2+(v2)2=√v24+v24=√2v24=√v22=v√2
Step 5: Determine the direction of the center of mass velocity
The direction of →Vcm can be determined using the components:
- The x-component is v2 (east direction).
- The y-component is v2 (north direction).
The angle θ with respect to the east direction can be calculated using:
tan(θ)=oppositeadjacent=v2v2=1
Thus, θ=45∘.
Conclusion
The magnitude of the velocity of the center of mass is v√2 and the direction is northeast.
Let’s denote the two particles:
- Particle 1 is moving due north with velocity →v1=v^j (where ^j is the unit vector in the north direction).
- Particle 2 is moving due east with velocity →v2=v^i (where ^i is the unit vector in the east direction).
Let both particles have the same mass m.
The velocity of the center of mass →Vcm is given by the formula:
→Vcm=m1→v1+m2→v2m1+m2
Since both particles have the same mass m:
→Vcm=m→v1+m→v2m+m=→v1+→v22
→Vcm=v^j+v^i2=v2^i+v2^j
To find the magnitude of →Vcm:
|→Vcm|=√(v2)2+(v2)2=√v24+v24=√2v24=√v22=v√2
The direction of →Vcm can be determined using the components:
- The x-component is v2 (east direction).
- The y-component is v2 (north direction).
tan(θ)=oppositeadjacent=v2v2=1
Thus, θ=45∘.
The magnitude of the velocity of the center of mass is v√2 and the direction is northeast.
Similar Questions
Two particles of masses 3kg and 2kg move due north and due east respectively with the velocities2ms−1and3ms−1. The magnitude and direction of the velocity of centre of mass is
View SolutionTwo particles of equal mass are moving along the same straight line with the same speed in opposite direction. What is the speed of the centre of mass of the system ?
View SolutionTwo particles of equal mass are moving along the same straight line with the same speed in opposite direction. What is the speed of the centre of mass of the system ?
View SolutionTwo identical particles move towards each other with velocity 2v and v, respectively. The velocity of the centre of mass is:
View SolutionA body of mass m moving with a constant velocity v hits another body of the same mass moving with the same velocity v but in the opposite direction and sticks to it. The velocity of the compound body after collision is
View SolutionTwo particles, A and B of masses m and 3m, are moving along X and Y axes respectively, with the same speed v. They collide at the origin, and coalesce into one body, after the c ollision. What is the velocity of this coalesced mass ?
View SolutionTwo partticles A and B intially at rest move towards each other under a mutual force of attraction. The instant at which velocity of A is 4v and velocity of B is 2v, the velocity of centre of mass of the system at that instant will be
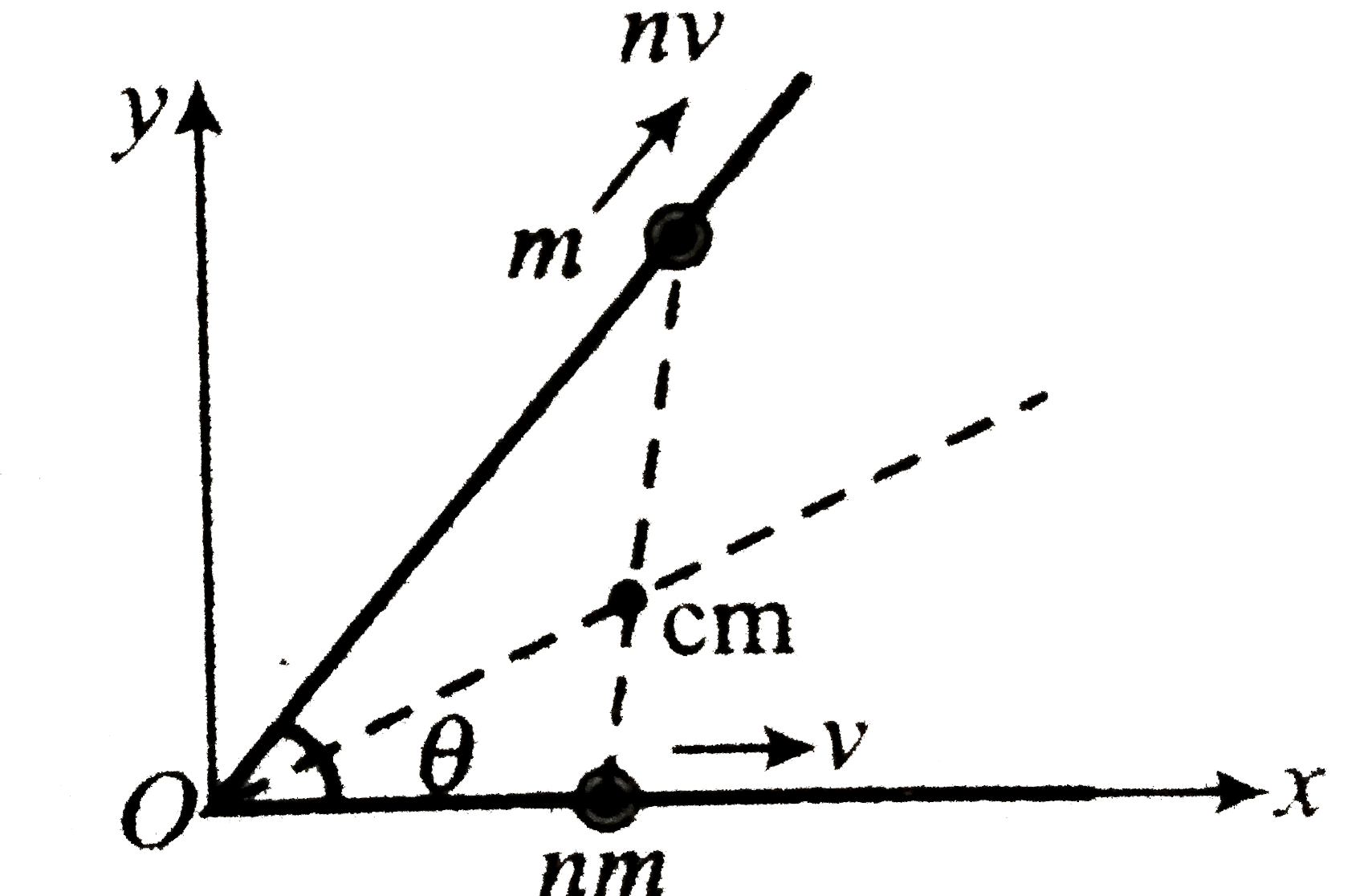
View SolutionTwo masses nm and m, start simultaneously from the intersection of two straight lines with velocities v and nv respectively. It is observed that the path of their centre of mass is a straight line bisecting the angle between the given straight lines. Find the magnitude of the velocity of centre of mass. [Here θ=angle between the lines]
View SolutionTwo particles of equal mass are moving along the same line with the same speed in the same direction. What is the speed of the centre of mass of the system ?
View SolutionTwo particles of equal mass are moving along the same line with the same speed in the same direction. What is the speed of the centre of mass of the system ?
View Solution