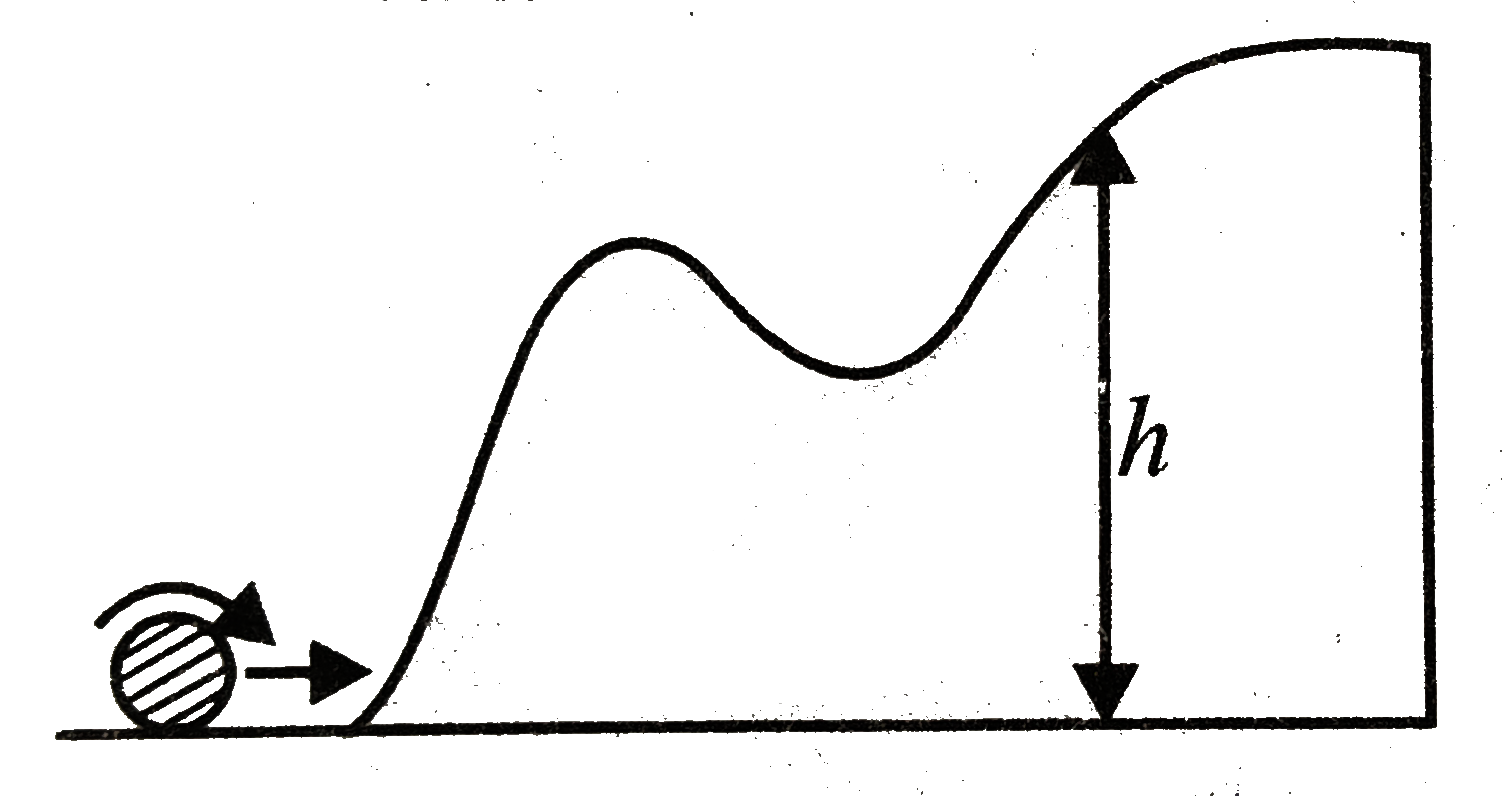
A body of mass M and radius r, rolling on a smooth horizontal floor with velocity v, rolls up an irregular inclined plane up to a vertical height (3v2/4g). Compute the moment of inertia of the body.
The total KE of the body
K=KT+KR=12mv2[1+Imr2]
When rolls up an inclined plane of height h=3V24g its KE is converted into PE
So 12mv2[1+Imr2]=mg(3v24g)
on simplification I=mr22 hence the body is either a disc or cylinder.
Similar Questions
An object of radius R and mass M is rolling horizontally without slipping with speed v . It then rolls up the hill to a maximum height h=3v24g . The moment of inertia of the object is ( g = acceleration due to gravity)
View SolutionA disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be:

View SolutionA uniform circular disc of mass m is set rolling on a smooth horizontal table with a uniform linear velocity v. Find the total K.E. of the disc.
View SolutionA body of radius R and mass m is rolling smoothly with speed v on a horizontal surface. It then rolls up a hill to a maximum height h. If h=3v2/4g. What might the body be ?
View SolutionWhen a body rolls without sliding up an inclined plane the frictional force is :
View SolutionA solid cylinder of mass M and radius R rolls without slipping on a flat horizontal surface. Its moment of inertia about the line of contact is
View SolutionA disc of mass m and radius R is rolling on horizontal ground with linear velocity v. What is the angular momentum of the disc about an axis passing through bottommost point and perpendicular to the plane of motion ?
View SolutionA mass m of radius r is rolling horizontally without any slip with a linear speed v. It then rolls up to a height given by 34v2g
View SolutionA body of mass m is thrown upwards at an angle θ with the horizontal with velocity v. While rising up the velocity of the mass after t second will be
View SolutionA cylinder of mass M and radius R rolls on an inclined plane. The gain in kinetic energy is
View Solution
