If the midpoint of the sides ¯¯¯¯¯¯BC,¯¯¯¯¯¯CA,¯¯¯¯¯¯AB of ΔABC are (3, -3), (3, -1), (1, 1) respectively then the vertices A, B, C are
The correct Answer is:(5,-5)
To find the vertices A, B, and C of triangle ΔABC given the midpoints of its sides, we can use the midpoint formula. The midpoints of sides BC, CA, and AB are given as follows:
- Midpoint of BC: MBC=(3,−3)
- Midpoint of CA: MCA=(3,−1)
- Midpoint of AB: MAB=(1,1)
Let the coordinates of the vertices be:
- A=(x1,y1)
- B=(x2,y2)
- C=(x3,y3)
Step 1: Use the Midpoint Formula
The midpoint formula states that the midpoint M of a line segment connecting points (x1,y1) and (x2,y2) is given by:
M=(x1+x22,y1+y22)
Step 2: Set Up Equations for Midpoints
Using the midpoints provided, we can set up the following equations:
1. For midpoint MBC:
x2+x32=3andy2+y32=−3
2. For midpoint MCA:
x3+x12=3andy3+y12=−1
3. For midpoint MAB:
x1+x22=1andy1+y22=1
Step 3: Solve for Coordinates
Now, we can solve these equations step by step.
From MBC:
1. x2+x3=6 (Multiplying the first equation by 2)
2. y2+y3=−6 (Multiplying the second equation by 2)
From MCA:
3. x3+x1=6 (Multiplying the first equation by 2)
4. y3+y1=−2 (Multiplying the second equation by 2)
From MAB:
5. x1+x2=2 (Multiplying the first equation by 2)
6. y1+y2=2 (Multiplying the second equation by 2)
Step 4: Substitute and Solve
Now we can substitute equations to find x1,x2,x3 and y1,y2,y3.
Solving for x-coordinates:
From equations (1) and (5):
- x2+x3=6 (1)
- x1+x2=2 (5)
Substituting x2=2−x1 into (1):
(2−x1)+x3=6⟹x3=6−2+x1=4+x1
Now substitute x3 into (3):
(4+x1)+x1=6⟹2x1+4=6⟹2x1=2⟹x1=1
Now substituting x1=1 back:
- From (5): 1+x2=2⟹x2=1
- From (1): 1+x3=6⟹x3=5
Thus, the x-coordinates are:
- x1=1
- x2=1
- x3=5
Solving for y-coordinates:
Using the same method:
From equations (2) and (6):
- y2+y3=−6 (2)
- y1+y2=2 (6)
Substituting y2=2−y1 into (2):
(2−y1)+y3=−6⟹y3=−6−2+y1=−8+y1
Now substitute y3 into (4):
(−8+y1)+y1=−2⟹2y1−8=−2⟹2y1=6⟹y1=3
Now substituting y1=3 back:
- From (6): 3+y2=2⟹y2=−1
- From (2): −1+y3=−6⟹y3=−5
Thus, the y-coordinates are:
- y1=3
- y2=−1
- y3=−5
Final Coordinates of Vertices
The vertices of triangle ΔABC are:
- A=(1,3)
- B=(1,−1)
- C=(5,−5)
Summary
The vertices of triangle ΔABC are:
- A(1,3)
- B(1,−1)
- C(5,−5)
- Midpoint of CA: MCA=(3,−1)
- Midpoint of AB: MAB=(1,1)
- A=(x1,y1)
- B=(x2,y2)
- C=(x3,y3)
The midpoint formula states that the midpoint M of a line segment connecting points (x1,y1) and (x2,y2) is given by:
M=(x1+x22,y1+y22)
Using the midpoints provided, we can set up the following equations:
x2+x32=3andy2+y32=−3
x3+x12=3andy3+y12=−1
x1+x22=1andy1+y22=1
Now, we can solve these equations step by step.
1. x2+x3=6 (Multiplying the first equation by 2)
2. y2+y3=−6 (Multiplying the second equation by 2)
3. x3+x1=6 (Multiplying the first equation by 2)
4. y3+y1=−2 (Multiplying the second equation by 2)
5. x1+x2=2 (Multiplying the first equation by 2)
6. y1+y2=2 (Multiplying the second equation by 2)
Now we can substitute equations to find x1,x2,x3 and y1,y2,y3.
From equations (1) and (5):
- x2+x3=6 (1)
- x1+x2=2 (5)
(2−x1)+x3=6⟹x3=6−2+x1=4+x1
(4+x1)+x1=6⟹2x1+4=6⟹2x1=2⟹x1=1
- From (5): 1+x2=2⟹x2=1
- From (1): 1+x3=6⟹x3=5
- x1=1
- x2=1
- x3=5
Using the same method:
From equations (2) and (6):
- y2+y3=−6 (2)
- y1+y2=2 (6)
(2−y1)+y3=−6⟹y3=−6−2+y1=−8+y1
(−8+y1)+y1=−2⟹2y1−8=−2⟹2y1=6⟹y1=3
- From (6): 3+y2=2⟹y2=−1
- From (2): −1+y3=−6⟹y3=−5
- y1=3
- y2=−1
- y3=−5
The vertices of triangle ΔABC are:
- A=(1,3)
- B=(1,−1)
- C=(5,−5)
The vertices of triangle ΔABC are:
- A(1,3)
- B(1,−1)
- C(5,−5)
Similar Questions
If D, E, F are the midpoints of the sides ¯¯¯¯¯¯BC,¯¯¯¯¯¯CA,¯¯¯¯¯¯AB of ΔABC where A =(-3, 4), B = (-1, -2), C = (5, 6) then the area of ΔDEF=
View SolutionThe coordinates of the mid points of sides AB, BC and CA of ABC are D(1,2,−3), E(3,0,1)and F(−1,1,−4) respectively. Write the coordinates of its centroid.
View Solution
Knowledge Check
In rectangle ABCD below ,¯¯¯¯¯¯BC is 16 inches long and ¯¯¯¯¯¯CD is 12 inches long . Points E,F and G are the midpoints of ¯¯¯¯¯¯AD,¯¯¯¯¯¯ABand¯¯¯¯¯¯BC respectively . What is the perimeter ,in inches , of pentagon CDEFG ?
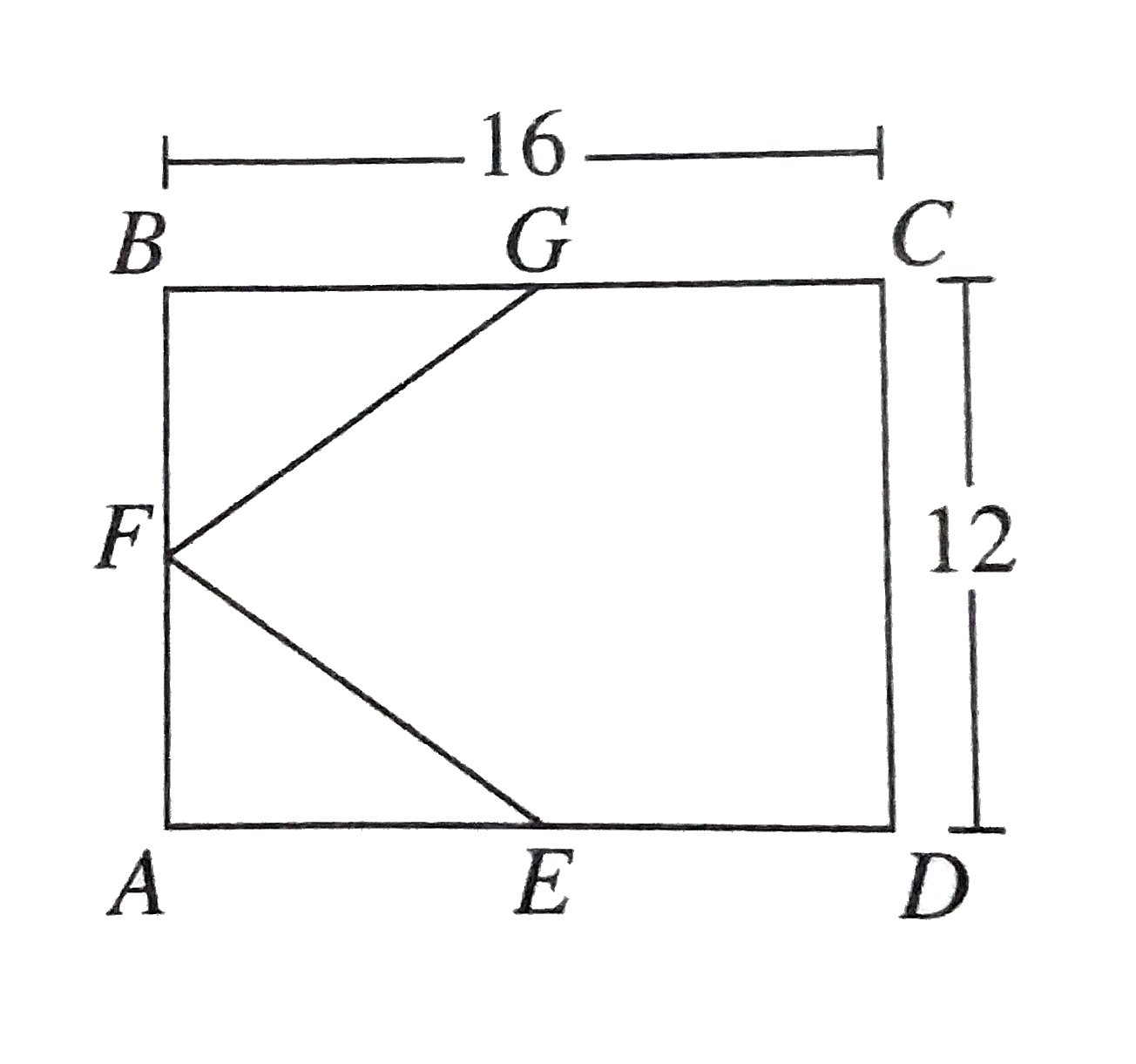 A48B56C96D144
A48B56C96D144
The coordinates of the mid points of sides AB, BC and CA of ABC are D(1,2,−3), E(3,0,1)and F(−1,1,−4) respectively. Write the coordinates of its centroid.
View SolutionThe altitudes from the angular points A,B, and C on the opposite sides BC, CA and AB of ΔABC are 210, 195 and 182 respectively. Then the value of a is ____
View SolutionIf the coordinates of midpoints of ABandACofΔ A B C are (3,5) and (-3,-3) respectively, then write the length of side BC.
View SolutionIf (2, 1), (-1, -2), (3, -3) are the mid points of the sides BC, CA, AB respectively of ΔABC, then the equation of the perpendicular bisector of AB is ax+by+c=0, then (a+b+c) is _______.
View SolutionThe vertices of a ΔABC are A(1, 1), B(7, 3) and C(3, 6). State the slope of the altitude to BC
View SolutionThe vertices of a ΔABC are A(1, 1), B(7, 3) and C(3, 6). State the slopr of the altitude to AB
View SolutionThe equations of the sides AB and CA of a ΔABC are x+2y=0 and x−y=3 respectively. Given a fixed point P(2, 3).
Q. If P be orthocentre of ΔABC then equation of side BC is :
View Solution

