A ray enters a glass sphere of refractive index μ=(√3) at an angle of incidence of 60∘, ray is reflected and refracted at the farther surface of the sphere. The angle between the reflected and refracted rays at this surface is
μ=sinisinr
∴sinr=siniμ=sin60∘√3=12
∴r=30∘,PC=QC,∴∠CPQ=∠PQC=∠r=30∘
Angle between refected ray QR and refracted ray QS at the other face =180∘−r−60∘=180∘−30∘−60∘=90∘

Similar Questions
A ray incident at a point at an angle of incidence of 60∘ enters a glass sphere with refractive index √3 and it is reflected and refracted at the farther surface of the sphere. The angle between the reflected and refracted rays at this surface is:
View SolutionA ray incident at a point at an angle of incidence of 60∘ enters a glass sphere with refractive index √3 and it is reflected and refracted at the farther surface of the sphere. The angle between the reflected and refracted rays at this surface is:
View Solution
Knowledge Check
A ray incident at a point at an angle of incidence of 60∘ enters a glass sphere with refractive index √3 and it is reflected and refracted at the farther surface of the sphere. The angle between the reflected and refracted rays at this surface is:
A50∘B60∘C90∘D40∘A ray of light strikes a transparent rectangular slab of refractive index √2 at an angle of incidence of 45∘. The angle betweent the reflected and refracted rays is
A75∘B90∘C105∘D120∘
A ray incident at an angle of incidence 60∘ enters a glass sphere of μ=√3 and it is reflected and refracted at the farther surface of the sphere. The angle between reflacted and refracted rays at this surface is
View SolutionA ray of light-is incident on glass at the polarising angle ip. Find the angle between the reflected and refracted rays.
View SolutionA ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?
View SolutionA ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?
View SolutionA light ray is incident on a glass sphere of reflective index μ=√3 at an angle of incidence 60∘ as shown in Fig. Find the angles r, r′ e and the total deviation after two refractions.
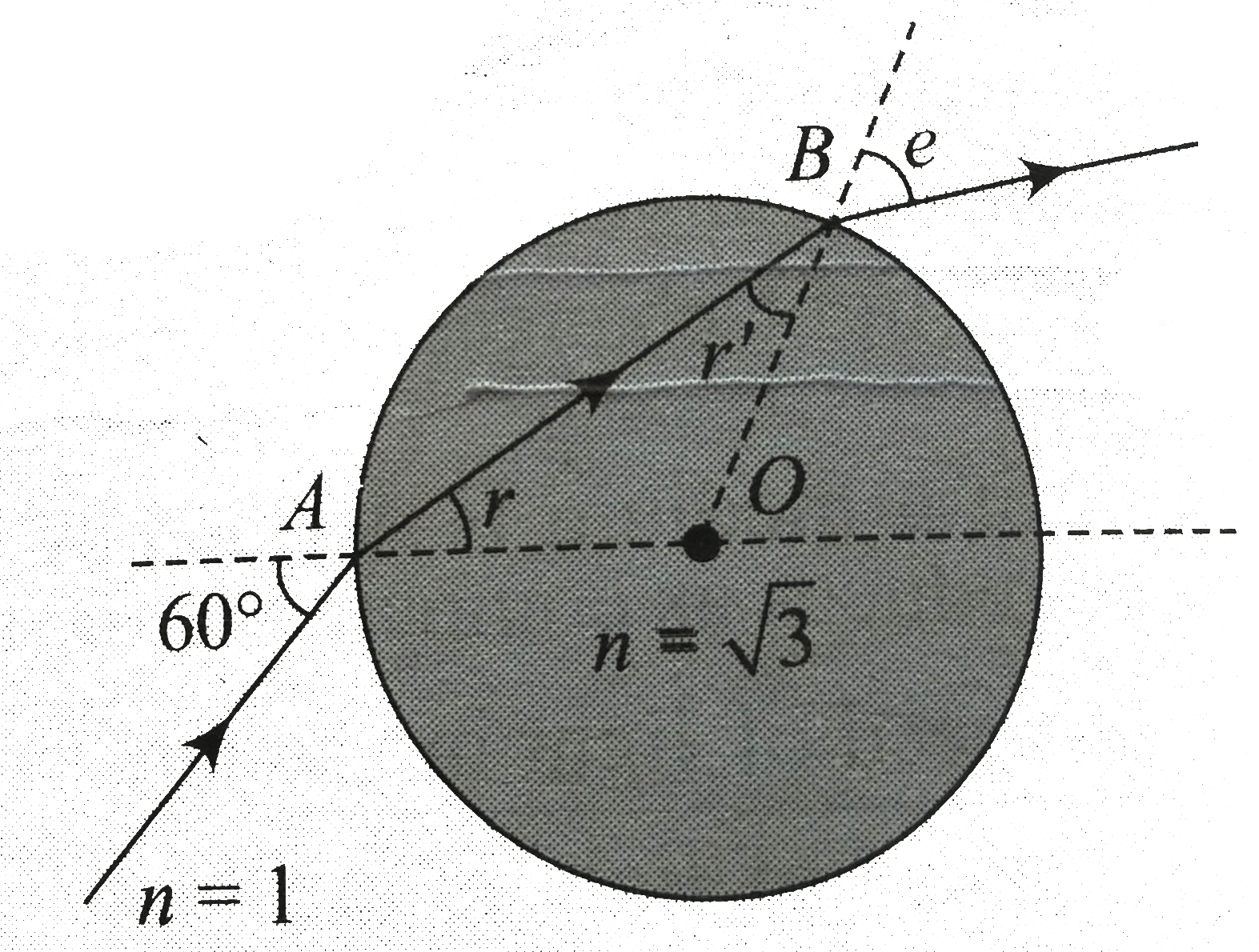
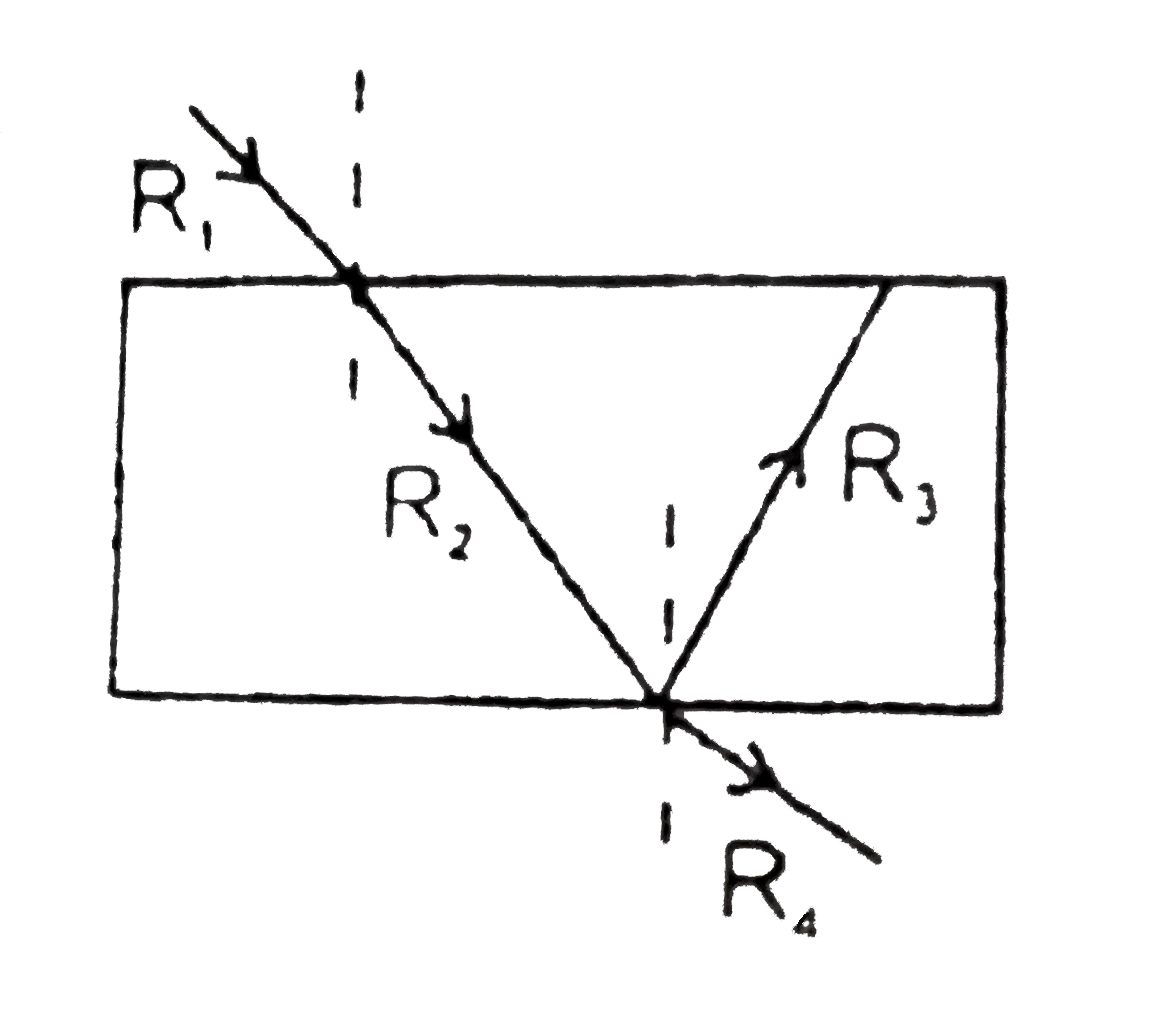
View SolutionA ray R1 is incident on the plane surface of the glass slab (kept in air) of refractive index √2 at angle of incident equal to the critical angle for this air glass system. The refracted ray R2 undergoes partial reflection & refraction at the other surface. The angle between the reflected ray R3 and the refracted ray R4 at that surface is :
View Solution