Consider a radioactive disintegration according to the equation A→B→C. Decay constant of A and B is same and equal to λ. Number of nuclei of A, B and C are N0 , 0, 0 respectively at t=0. Find
(a) number of nuclei of B as function of time t.
(b) time t at which the activity of B is maximum and the value of maximum activity of B.
The correct Answer is:(a) NB=λN0(te−λt) (b) t=1λ,Rmax=λN0e
Step by step video solution for Consider a radioactive disintegration according to the equation ArarrBrarrC. Decay constant of A and B is same and equal to lambda. Number of nuclei of A, B and C are N_0 , 0, 0 respectively at t=0. Find (a) number of nuclei of B as function of time t. (b) time t at which the activity of B is maximum and the value of maximum activity of B. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Two radioactive materials A & B have decay constant 3λ and 2λ respectively. At t=0 the numbers of nuclei of A and B are 4N0 and 2N0 respectively then,
View SolutionNumber of nuclei of a radioactive substance are 1000 and 900 at times t=0 and time t=2s. Then, number of nuclei at time t=4s will be
View Solution
Knowledge Check
The decay constant of a radioactive isotope is λ. If A1 and A2 are its activites at time t1 and t2 respectively, then the number of nuclei which have decayed the time (t1−t2)
AA1t1−A2t2BA1−A2C(A1−A2)/λDλ(A1−A2)
At time t=0 , number of nuclei of a radioactive substance are 100. At t=1 s these numbers become 90. Find the number of nuclei at t=2s.
View SolutionAt time t=0 , number of nuclei of a radioactive substance are 100. At t=1 s these numbers become 90. Find the number of nuclei at t=2s.
View SolutionNucleus A decays into B with a decay constant λ1 and B further decays into C with a decay constant λ2 . Initially, at t = 0, the number of nuclei of A and B were 3N0 and N0 respectively. If at t = t0 number of nuclei of B becomes constant and equal to 2N0, then
View SolutionA radio nuclide X is produced at constant rate α. At time t=0, number of nuclei of X are zero. Find
(a) the maximum number of nuclei of X.
the number of nuclei at time t.
Decay constant of X is λ.
View SolutionTwo radioactive samples of different elements (half-lives t1 and t2 respectively) have same number of nuclei at t=0. The time after which their activities are same is
View SolutionNucleus A decays to B with decay constant λ1 and B decays to C with decay constant λ2. Initially at t=0 number of nuclei of A and B are 2N0 and N0 respectively. At t=to, no. of nuclei of B is 3N02 and nuclei of B stop changing. Find t0?
View SolutionConsider radioactive decay of A to B with which further decays either to X or Y, λ1,λ2 and λ3 are decay constant for A to B decay, B to X decay and Bto Y decay respectively. At t=0, the number of nuclei of A,B,X and Y are N0,N0 zero and zero respectively.
N1,N2,N3 and N4 are the number of nuclei of A,B,X and Y at any instant t.
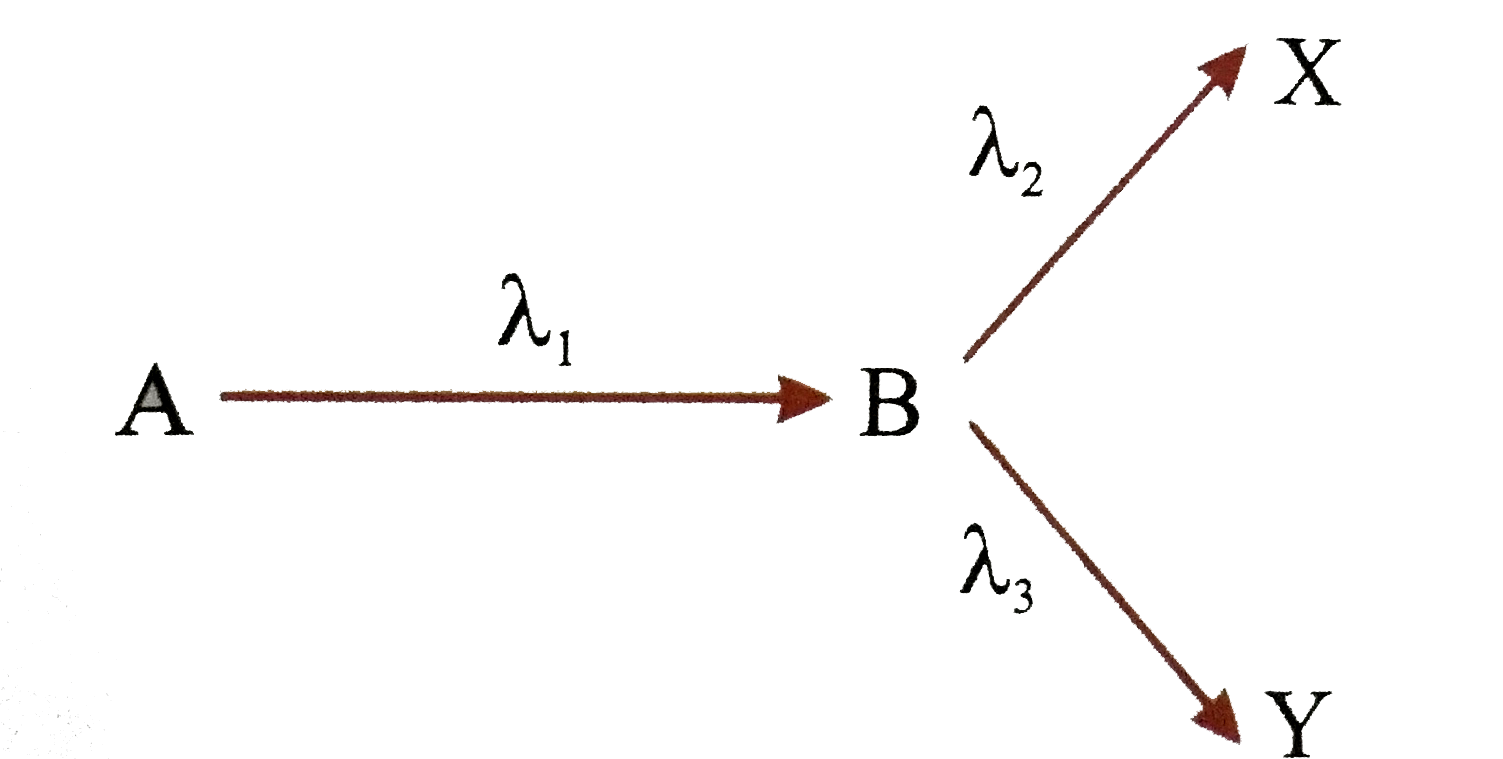
The number of nuclei of B will first increase and then after a maximum value, it decreases for
View Solution
