A capacitor, charged to 10 V , is being discharged through a resistance R. At the end of 1s the voltage across the capacitor is 5V. What will be the voltage after 2s ?
To solve the problem of a capacitor discharging through a resistor, we can use the formula for the voltage across a discharging capacitor:
V(t)=V0e−tRC
where:
- V(t) is the voltage across the capacitor at time t,
- V0 is the initial voltage (10 V in this case),
- R is the resistance,
- C is the capacitance,
- t is the time in seconds.
Step 1: Understand the given information
We know:
- Initial voltage V0=10V
- Voltage after 1 second V(1)=5V
Step 2: Use the discharging formula at t=1 second
Using the discharging formula at t=1:
V(1)=V0e−1RC
Substituting the known values:
5=10e−1RC
Step 3: Solve for the exponent
Dividing both sides by 10:
0.5=e−1RC
Taking the natural logarithm of both sides:
ln(0.5)=−1RC
Step 4: Express RC
From the above equation, we can express RC:
RC=−1ln(0.5)
Step 5: Calculate the voltage at t=2 seconds
Now, we need to find the voltage at t=2:
V(2)=V0e−2RC
Substituting RC from the previous step:
V(2)=10e−2−1ln(0.5)
V(2)=10e2ln(0.5)
Step 6: Simplify the expression
Using the property of logarithms:
e2ln(0.5)=(eln(0.5))2=(0.5)2=0.25
So,
V(2)=10×0.25=2.5V
Final Answer
The voltage across the capacitor after 2 seconds will be 2.5V.
---
- V(t) is the voltage across the capacitor at time t,
- V0 is the initial voltage (10 V in this case),
- R is the resistance,
- C is the capacitance,
- t is the time in seconds.
We know:
- Initial voltage V0=10V
- Voltage after 1 second V(1)=5V
Using the discharging formula at t=1:
V(1)=V0e−1RC
Substituting the known values:
5=10e−1RC
Dividing both sides by 10:
0.5=e−1RC
ln(0.5)=−1RC
From the above equation, we can express RC:
RC=−1ln(0.5)
Now, we need to find the voltage at t=2:
V(2)=V0e−2RC
V(2)=10e−2−1ln(0.5)
V(2)=10e2ln(0.5)
Using the property of logarithms:
e2ln(0.5)=(eln(0.5))2=(0.5)2=0.25
V(2)=10×0.25=2.5V
The voltage across the capacitor after 2 seconds will be 2.5V.
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:AAKASH SERIESChapter:CURRENT ELECTRICITYExercise:EXERCISE (LONG ANSWER QUESTIONS)
Explore 12 Videos
- CURRENT ELECTRICITYBook:AAKASH SERIESChapter:CURRENT ELECTRICITYExercise:EXERCISE (SHORT ANSWER QUESTIONS)
Explore 12 Videos
- COMMUNICATION SYSTEMS Book:AAKASH SERIESChapter:COMMUNICATION SYSTEMS Exercise:PRACTICE EXERCISE (TV Antenna)
Explore 16 Videos
- CURRENT ELECTRICITYBook:AAKASH SERIESChapter:CURRENT ELECTRICITYExercise:EXERCISE - IA
Explore 2 Videos
Similar Questions
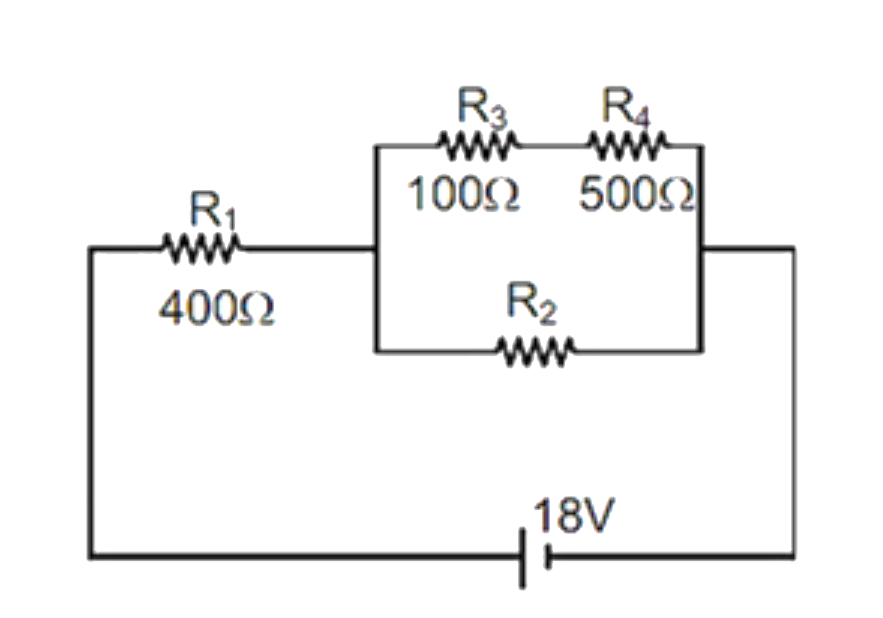
If the voltage across 500Ω is 5 V. then R2 is
View SolutionA capacitor is charged to a certain potential and then allowed to discharge through a resistance R. The ratio of charge on the capacitor to current in the circuit
View SolutionA capacitor of 0.75μF is charged to a voltage of 16 V. What is the magnitude of the charge on each plate of the capacitor ?
View SolutionA capacitor charged to 50V is discharged by connecting the two plates at t=0.If the potential difference across the plates drops to 1.0 V at t=10 ms,what will be the potential difference at t=20 ms?
View SolutionA 100μF capacitor is charged to 100V. After the charging, battery is disconnected. The capacitor is then connected in parallel to another capacitor. The final voltage is 20V. Calculate the capacity of second capacitor.
View SolutionA capacitor is connected to a 12 V battery through a resistance of (10Ω).It is found that the potential difference across the capacitor rises to 4.0 V in 1(mu)s. find the capacitance of the capacitor.
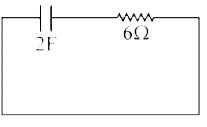
View SolutionIf the capacitor shown in the circuit is charged to 5V and left in the circuit, in 12s the charge on the capacitor will become:
View SolutionAn uncharged capacitor is connected to a 15 V battery through a resistance of 10Ω. It is found that in a time of 2μs, potential difference across the capacitor becomes 5V. Find the capacitance of the Capacitor. Take ln(1.5) = 0.4.
View SolutionAn inductor L is allowed to discharge through capacitor C. The emf induced across the inductance when the capacitor is fully charged is
View SolutionAn ac source of 50 V (r.m.s value) is connected across a series R - C circuit. If the r.m.s voltage across the resistor is 40 V, then the r.m.s voltage across the capacitor is
View Solution