When 16 wires which are identical are connected in series, the effective resistance exceeds that when they are in parallel by 3178ΩThen the resistance of each wire is
0.5Ω
1Ω
2Ω
8Ω
The correct Answer is:C
To solve the problem, we need to find the resistance of each wire when 16 identical wires are connected in series and in parallel, and the difference in effective resistance is given.
1. Define Variables:
Let the resistance of each wire be r.
2. Calculate Series Resistance:
When 16 wires are connected in series, the total resistance Rs is given by:
Rs=16r
3. Calculate Parallel Resistance:
When the same 16 wires are connected in parallel, the total resistance Rp is given by:
Rp=r16
4. Set Up the Equation:
According to the problem, the effective resistance in series exceeds that in parallel by 3178 ohms. We can express this as:
Rs=Rp+3178
Converting 3178 to an improper fraction:
3178=31×8+78=248+78=2558
Thus, we can rewrite the equation as:
16r=r16+2558
5. Clear the Fractions:
To eliminate the fractions, multiply the entire equation by 16:
16×16r=16×r16+16×2558
This simplifies to:
256r=r+510
6. Rearrange the Equation:
Now, rearranging gives:
256r−r=510
255r=510
7. Solve for r:
Divide both sides by 255:
r=510255=2 ohms
Conclusion:
The resistance of each wire is 2 ohms.
Let the resistance of each wire be r.
When 16 wires are connected in series, the total resistance Rs is given by:
Rs=16r
When the same 16 wires are connected in parallel, the total resistance Rp is given by:
Rp=r16
According to the problem, the effective resistance in series exceeds that in parallel by 3178 ohms. We can express this as:
Rs=Rp+3178
Converting 3178 to an improper fraction:
3178=31×8+78=248+78=2558
Thus, we can rewrite the equation as:
16r=r16+2558
To eliminate the fractions, multiply the entire equation by 16:
16×16r=16×r16+16×2558
This simplifies to:
256r=r+510
Now, rearranging gives:
256r−r=510
255r=510
Divide both sides by 255:
r=510255=2 ohms
The resistance of each wire is 2 ohms.
Topper's Solved these Questions
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MOVING CHANGES & MEGNETISM)
95 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )
52 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (ELECTRIC POTENTIAL & CAPACITANCE )
143 Videos
- ALTERNATING CURRENTBOOK - AAKASH SERIESCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE - III
24 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION
128 Videos
Similar Questions
A set of n identical resistors, each of resistance RΩ, when connected in series have an effective resistance XΩ and when the resistors are connected in parallel, their effective resistance is YΩ. Find the relation between R, X and Y.
View SolutionFour resistors each of resistance 2 Ω are connected in parallel. What is the effective resistance ?
View SolutionThe Total resistance when connected in series in 9Ω and when connected in parallel is 2Ω The value of two resistance are
View SolutionWhen a resistance wire is passed through a die the cross-section area decreases by 1%, the change in resistance of the wire is
View SolutionResistance of 100Ω and 200Ω are connected in series with 220 V mains. When a voltmeter of 1000Ω resistance is connected in parallel to100Ω , then the reading of voltmeter is
View SolutionAssertion : A resistance wire is broken into four pices and all are connected in parallel. Then, net resistance becomes 1/16 times.
Reason : In parallel net resistance is less than the smallest value of individual resistance.
View SolutionA wire has resistance of 24Ω is bent in the following shape. The effective resistance between A and B is
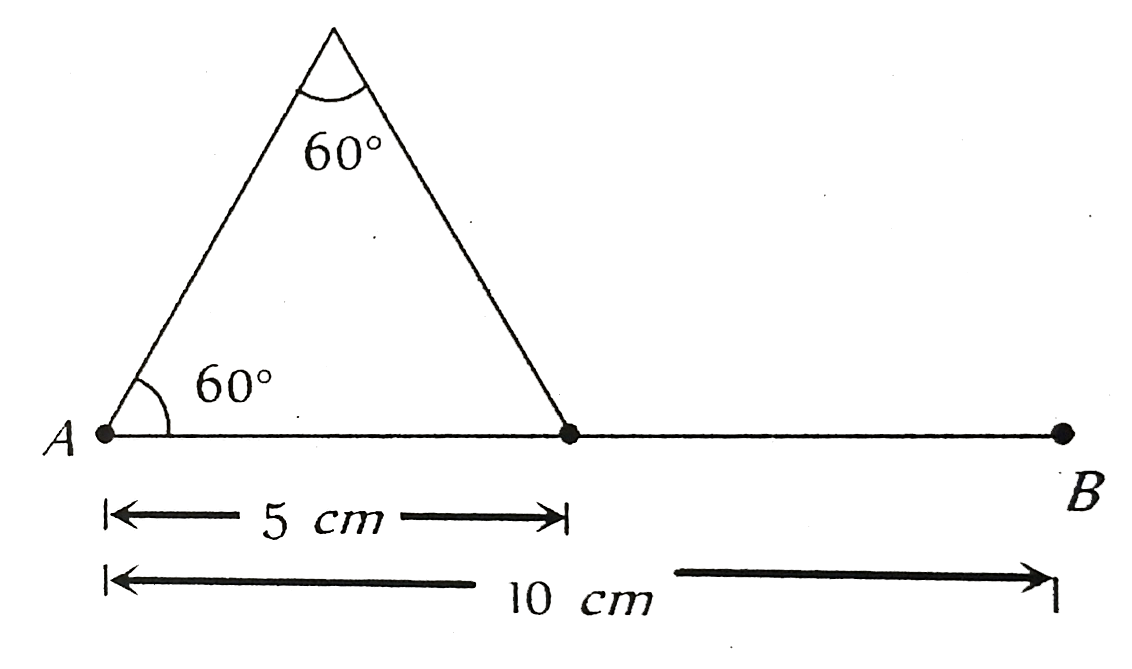
View SolutionA carbon and an aluminium wire are connected in series. If the combination has equivalent resistance of(90Ω) at (0∘C), the value of the resistance of each wire at(0∘C) so that the resistance of combination does not change with temperature is
View SolutionThe resultant resistance of two resistance in series is 50 Ω and it is 12 Ω , when they are in parallel. The individual resistances are
View SolutionPotentiometer wire of length 1m is connected in series with 490Ω resistance and 2V battery. If 0.2mVcm is the potential gradient, then resistance of the potentiameter wire is approximately
View Solution
