There are three concentric thin spherical shells A, B and C of radii R, 2R, and 3R. Shells A and Care given charges q and 2q and shell B is earthed. Then which of the given is correct ?
charge on inner surface of shell C is 43q
charge on outer surface of shell B is −43 q
charge on outer surface of shell C is 23q
all the above
The correct Answer is:D
To solve the problem, we need to analyze the charges on the three concentric spherical shells A, B, and C, given that shell B is earthed. Here’s a step-by-step solution:
Step 1: Understand the Setup
We have three concentric spherical shells:
- Shell A with radius R and charge q
- Shell B with radius 2R which is earthed (potential = 0)
- Shell C with radius 3R and charge 2q
Step 2: Analyze Shell B (Earthed)
Since shell B is earthed, the potential on its surface must be zero. This means that the total charge on shell B must balance the charges from shells A and C.
Step 3: Determine Charge on Shell B
Let Q′ be the charge on the outer surface of shell B. The inner surface of shell B will have a charge of −q (to balance the charge from shell A) and −2q (to balance the charge from shell C). Therefore, the total charge on the inner surface of shell B is:
Qinner,B=−q−2q=−3q
Since the total charge on shell B must be zero (as it is earthed), we have:
Q′+(−3q)=0⟹Q′=3q
Step 4: Determine Charge on Shell C
The charge on the inner surface of shell C must balance the charge on the outer surface of shell B. Since the outer surface of shell B has a charge of 3q, the inner surface of shell C will have a charge of +3q.
The total charge on shell C is 2q, so the charge on the outer surface of shell C will be:
Qouter,C=2q−3q=−q
Step 5: Final Charges on Each Shell
- Shell A:
- Inner surface: 0
- Outer surface: q
- Shell B:
- Inner surface: −3q
- Outer surface: 3q
- Shell C:
- Inner surface: +3q
- Outer surface: −q
Conclusion
Now we can summarize the charges:
1. Charge on inner surface of shell C: +3q
2. Charge on outer surface of shell B: 3q
3. Charge on outer surface of shell C: −q
Since all calculations are consistent with the problem statement, the correct answer is that all the options provided are correct.
We have three concentric spherical shells:
- Shell A with radius R and charge q
- Shell B with radius 2R which is earthed (potential = 0)
- Shell C with radius 3R and charge 2q
Since shell B is earthed, the potential on its surface must be zero. This means that the total charge on shell B must balance the charges from shells A and C.
Let Q′ be the charge on the outer surface of shell B. The inner surface of shell B will have a charge of −q (to balance the charge from shell A) and −2q (to balance the charge from shell C). Therefore, the total charge on the inner surface of shell B is:
Qinner,B=−q−2q=−3q
Since the total charge on shell B must be zero (as it is earthed), we have:
Q′+(−3q)=0⟹Q′=3q
The charge on the inner surface of shell C must balance the charge on the outer surface of shell B. Since the outer surface of shell B has a charge of 3q, the inner surface of shell C will have a charge of +3q.
Qouter,C=2q−3q=−q
- Shell A:
- Inner surface: 0
- Outer surface: q
- Shell B:
- Inner surface: −3q
- Outer surface: 3q
- Shell C:
- Inner surface: +3q
- Outer surface: −q
Now we can summarize the charges:
1. Charge on inner surface of shell C: +3q
2. Charge on outer surface of shell B: 3q
3. Charge on outer surface of shell C: −q
Topper's Solved these Questions
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (CUTTENT ELECTRICITY )
108 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MOVING CHANGES & MEGNETISM)
95 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )
52 Videos
- ALTERNATING CURRENTBOOK - AAKASH SERIESCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE - III
24 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION
128 Videos
Similar Questions
Figure shows three concentric thin spherical shells A, B and C of radii a, b, and c. The shells A and C are given charge q and -q, respectively, and shell B is earthed. Then,
View SolutionFigure shows three concentric thin spherical shells A, B and C of radii a, b and c respectively. The shells A and C are given charges q and -q respectively and the shell B is earthed. Find the charges appearing on the surfaces of B and C.

View SolutionFigure shows three concentric thin spherical shells A, B and C of radii a, b and c respectively. The shells A and C are given charges q and -q respectively and the shell B is earthed. Find the charges appearing on the surfaces of B and C.

View SolutionThere are four concentric shells A,B, C and D of radii a,2a,3a and 4a respectively. Shells B and D are given charges +q and −q respectively. Shell C is now earthed. The potential difference VA−VC is k=(14πε0)
View SolutionThere are four concentric shells A,B, C and D of radii a,2a,3a and 4a respectively. Shells B and D are given charges +q and −q respectively. Shell C is now earthed. The potential difference VA−VC is k=(14πε0)
View SolutionThere are four concentric shells A,B, C and D of radii a,2a,3a and 4a respectively. Shells B and D are given charges +q and −q respectively. Shell C is now earthed. The potential difference VA−VC is k=(14πε0)
View SolutionThere are four concentric shells A,B, C and D of radii a,2a,3a and 4a respectively. Shells B and D are given charges +q and −q respectively. Shell C is now earthed. The potential difference VA−VC is k=(14πε0)
View SolutionFour concentric conducting spherical shells A, B, C and D of radii a, 2a, 3a and 4a respectively. Shell B and D are given charges q and −q respectively. If shell C is grounded then potential difference (VA — VC) is
View SolutionThere are three conducting and concentricspherical shells of radii R,2R and 3R. The charge on inner and outer most shells are q and 3q while middle shell is earthed. Find the ratio of number of field lines emitted by outermost shell and inner shell.
View Solution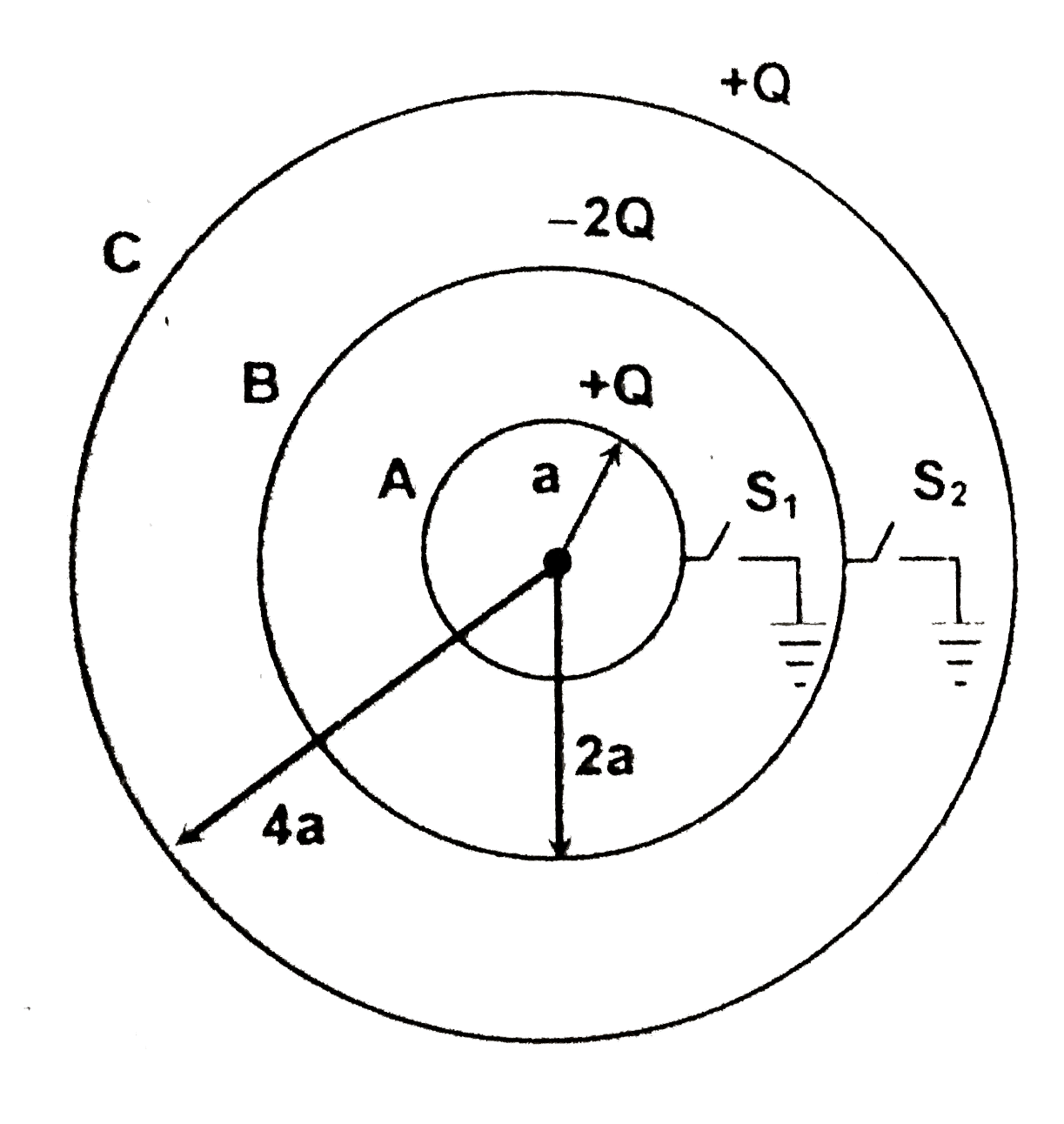
Three concentric spherical conducting shells A, B and C of radii a, 2a and 4a are initially given charges +Q, -2Q and +Q respectively. The charge on the middle spherical shell B after switches S1 and S2 are simultaneously closed, will be
View Solution
