Let P(r)=QπR4r be the charge desntiy distribution for a solid sphere of radius R and total charge Q. for a point 'p' inside the sphere at distance r1 from the centre of the sphere, the magnitude of electric field is
Qr213πeπs0R4
Q4πε0r21
Qr214πeπs0R4
0
The correct Answer is:C
Step by step video solution for Let P(r) = (Q)/(pi R^(4)) r be the charge desntiy distribution for a solid sphere of radius R and total charge Q. for a point 'p' inside the sphere at distance r_(1) from the centre of the sphere, the magnitude of electric field is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (ELECTRIC POTENTIAL & CAPACITANCE )
143 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (CUTTENT ELECTRICITY )
108 Videos
- ALTERNATING CURRENTBOOK - AAKASH SERIESCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE - III
24 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION
128 Videos
Similar Questions
Let P(r)=QπR4r be the charge density distribution for a solid sphere of radius R and total charge Q. For a point 'p' inside the sphere at distance r1 from the centre of the sphere, the magnitude of electric field is:
View SolutionA hallow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre:
View Solution
Knowledge Check
Let ρ(r)=QrπR4 be the charge density distribution for a soild sphere of radius R and total charge Q. For a point P inside the sphere at a distance r1 from the centre of the sphere, the magnitude of electric field is
AQr214πε0R4BQr213πε0R4C0DQ4iε0r21The radius of gyration of a solid sphere of radius R about a certain axis is also equal to R. If r is the distance between the axis and the centre of the sphere, then r is equal to
ARB0.5RC√0.6RD√0.3R
A conducting sphere of radius R is charged to a potential of V volts. Then the electric field at a distance r(>R) from the centre of the sphere would be
View SolutionA non-conducting solid sphere of radius R is uniformly charged. The magnitude of the electric filed due to the sphere at a distance r from its centre
View SolutionA solid insulating sphere of radius R is given a charge Q. If at a point inside the sphere the potential is 1.5 times the potential at the surface, this point will be
View SolutionA conducting sphere of radius R is given a charge Q. The electric potential and the electric field at the centre of the sphere respectively are
View SolutionA conducting sphere of radius R is given a charge Q. The electric potential and the electric field at the centre of the sphere respectively are
View SolutionIn the shown figure, the charge appearing on the conducting shell (grounded) of Radius R, when a point charge q is kept at a distance of d from the centre of the sphere is:
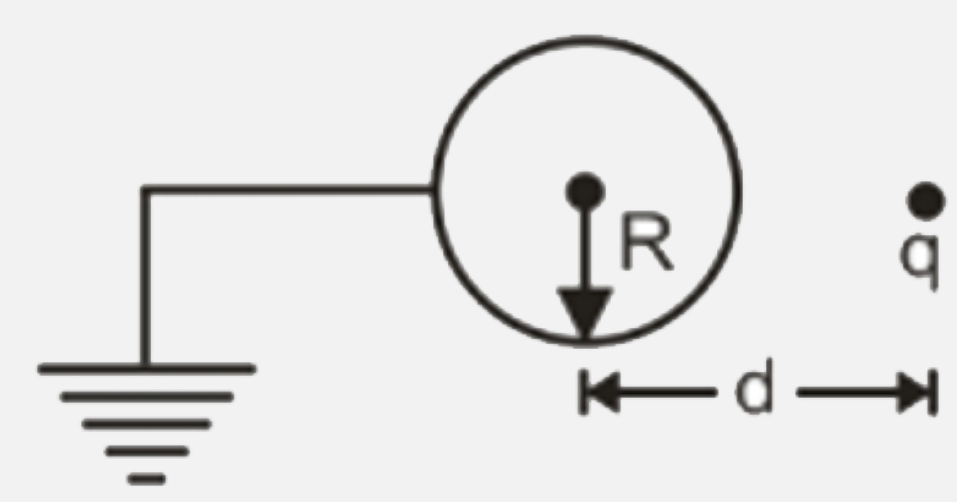
View Solution
