Two similar metal spheres are suspended by silk threads from the same point. When the spheres are given equal charges of 2μC the distance between them becomes 6cm. If length of each thread is 5 cm, the mass of each sphere is (g=10 m/s2)
4 kg
3kg
43kg
13 kg
The correct Answer is:C
To solve the problem, we need to analyze the forces acting on the two charged spheres suspended by silk threads. Here's a step-by-step solution:
Step 1: Understand the Setup
We have two identical metal spheres, each with a charge of q=2μC=2×10−6C. The distance between the spheres when charged is r=6cm=0.06m. The length of each thread is L=5cm=0.05m. The acceleration due to gravity is g=10m/s2.
Step 2: Draw a Diagram
Draw a diagram showing the two spheres, the threads, and the angles involved. Label the angles as θ. The distance between the spheres is 6cm, and each thread makes an angle θ with the vertical.
Step 3: Identify Forces
Each sphere experiences:
- Gravitational force Fg=mg acting downward.
- Tension T in the thread acting along the thread.
- Electrostatic force Fe acting horizontally due to the charges on the spheres.
Step 4: Resolve Forces
From the diagram:
- The vertical component of tension: Tcosθ=mg
- The horizontal component of tension: Tsinθ=Fe
Step 5: Express Electrostatic Force
The electrostatic force between the two charges is given by Coulomb's law:
Fe=kq2r2
where k=9×109Nm2/C2.
Step 6: Calculate Electrostatic Force
Substituting the values:
Fe=9×109(2×10−6)2(0.06)2
Calculating Fe:
Fe=9×1094×10−120.0036=9×109×43.6×10−12
Fe=10×10−3=0.01N
Step 7: Use Trigonometric Relationships
From the geometry of the setup, we can relate tanθ:
tanθ=34(since the horizontal distance is half of 6 cm, which is 3 cm, and the vertical distance is 4 cm)
Step 8: Substitute into Force Equations
Using tanθ=mgFe:
34=mg0.01
Substituting g=10m/s2:
34=m⋅100.01
m=3×0.014×10=0.0340=0.00075kg=0.75g
Final Answer
The mass of each sphere is 0.75g.
We have two identical metal spheres, each with a charge of q=2μC=2×10−6C. The distance between the spheres when charged is r=6cm=0.06m. The length of each thread is L=5cm=0.05m. The acceleration due to gravity is g=10m/s2.
Draw a diagram showing the two spheres, the threads, and the angles involved. Label the angles as θ. The distance between the spheres is 6cm, and each thread makes an angle θ with the vertical.
Each sphere experiences:
- Gravitational force Fg=mg acting downward.
- Tension T in the thread acting along the thread.
- Electrostatic force Fe acting horizontally due to the charges on the spheres.
From the diagram:
- The vertical component of tension: Tcosθ=mg
- The horizontal component of tension: Tsinθ=Fe
The electrostatic force between the two charges is given by Coulomb's law:
Fe=kq2r2
where k=9×109Nm2/C2.
Substituting the values:
Fe=9×109(2×10−6)2(0.06)2
Calculating Fe:
Fe=9×1094×10−120.0036=9×109×43.6×10−12
Fe=10×10−3=0.01N
From the geometry of the setup, we can relate tanθ:
tanθ=34(since the horizontal distance is half of 6 cm, which is 3 cm, and the vertical distance is 4 cm)
Using tanθ=mgFe:
34=mg0.01
Substituting g=10m/s2:
34=m⋅100.01
m=3×0.014×10=0.0340=0.00075kg=0.75g
The mass of each sphere is 0.75g.
Topper's Solved these Questions
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (ELECTRIC POTENTIAL & CAPACITANCE )
143 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (CUTTENT ELECTRICITY )
108 Videos
- ALTERNATING CURRENTBOOK - AAKASH SERIESCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE - III
24 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION
128 Videos
Similar Questions
Two small spheres, each of mass 0.1 gm and carrying same charge 10−9C are suspended by threads of equal length from the same point. If the distance between the centres of the sphere is 3 cm, then find out the angle made by the thread with the vertical. (g=10m/s2) & tan−1(1100)=0.6º
View SolutionTwo identical small equally charged conducting balls are suspended from long threads secured at one point. The charges and masses of the balls are such that they are in equilibrium when the distance between them is a(the length of thread L>>a). Then one of the balls is discharged. what will be the distance b(b<<L) between the balls when equilibrium is restored?
View SolutionThe centre of two identical spheres are 1.0 m apart . If the gravitational force between the spheres be 1.0 N , then what is the mass of each sphere ?
(G=6.67×10−11m3kg−1s−2) .
View SolutionTwo identical charged spheres are suspended by strings of equal lengths. The strings make an angle of 30∘ with each other. When suspended in a liquid of density 0.8gcm−3, the angle remains the same. If density of the material of the sphere is 1.6gcm−3, the dielectric constant of the liquid is
View SolutionTwo identical charged spheres are suspended by strings of equal lengths. The strings make an angle of 30∘ with each other. When suspended in a liquid of density 0.8gcm−3, the angle remains the same. If density of the material of the sphere is 1.6gcm−3, the dielectric constant of the liquid is
View SolutionA spherical capacitor has an inner sphere of radius 12 cm and an outer sphere of radius 13 cm. The outer sphere is earthed and the inner sphere is given a charge of 2.5μC. The space between the concentric spheres is filled with a liquid of dielectric constant 32.
(a) Determine the capacitance of the capacitor. (b) What is the potential of the inner sphere ?
(c) Compare the capacitance of this capacitor with that of an isolated sphere of radius 12 cm.Explain why the later is much smaller ?
View SolutionTwo small spheres each of mass m and charge q are tied from the same rigid support with the help of silk threads of length L. They make angle θ with the vertical as shown in the fig. If length L is decreased, then angle θ with the vertical.
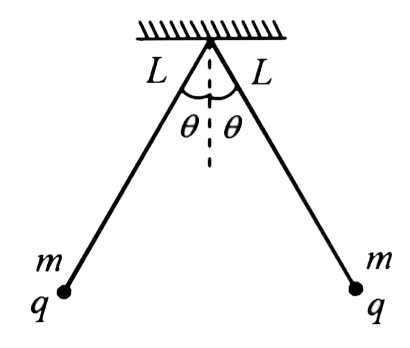
View SolutionA sherical capacitor has an inner sphere of radius 12cm and an outer spere of radius 13cm. The outer sphere is earthed, and the inner sphere is given a charge of 2.5μC. The space between the concentric spjheres is filled with a liquid of dielectric caonstant 32. Determine the potential of the inner sphere.
View SolutionTwo small spheres, each having a mass of 20 g, are suspended form a common point by two insulating strings of length 40 cm each. The spheres are identically charged and the speration between the balls at equilibrium is found to be 4 cm . Find the charge on each sphere.
View SolutionTwo isolated metallic spheres of radii 2 cm and 4 cm are given equal charge, then the ratio of charge density on the surfaces of the spheres will be
View Solution

