A cylindrical vessel of depth 4m is fully filled with non homogenious liquid whose refractive index varies with depth y (in meters) a . Find the depth of the bottom of vessel as seen by an observer just above the top of the vessel.
To solve the problem of finding the apparent depth of the bottom of a cylindrical vessel filled with a non-homogeneous liquid, we can follow these steps:
1. Understand the Given Information:
- The depth of the cylindrical vessel, h=4 m.
- The refractive index μ varies with depth y as μ=1+y4.
2. Identify the Formula for Apparent Depth:
- The formula for apparent depth d′ in a medium with varying refractive index is given by:
d′=∫h0dyμ(y)
- Here, μ(y)=1+y4.
3. Set Up the Integral:
- Substitute μ(y) into the integral:
d′=∫40dy1+y4
4. Simplify the Integral:
- Rewrite the integrand:
d′=∫40dy4+y4=∫4044+ydy
5. Evaluate the Integral:
- The integral can be evaluated as follows:
d′=4∫4014+ydy
- The integral ∫14+ydy is ln|4+y|.
- Thus,
d′=4(ln(4+y))40
- Evaluating the limits:
d′=4(ln(8)−ln(4))=4ln(84)=4ln(2)
6. Final Result:
- Therefore, the apparent depth of the bottom of the vessel as seen by an observer just above the top of the vessel is:
d′=4ln(2) meters
- The depth of the cylindrical vessel, h=4 m.
- The refractive index μ varies with depth y as μ=1+y4.
- The formula for apparent depth d′ in a medium with varying refractive index is given by:
d′=∫h0dyμ(y)
- Here, μ(y)=1+y4.
- Substitute μ(y) into the integral:
d′=∫40dy1+y4
- Rewrite the integrand:
d′=∫40dy4+y4=∫4044+ydy
- The integral can be evaluated as follows:
d′=4∫4014+ydy
- The integral ∫14+ydy is ln|4+y|.
- Thus,
d′=4(ln(4+y))40
- Evaluating the limits:
d′=4(ln(8)−ln(4))=4ln(84)=4ln(2)
- Therefore, the apparent depth of the bottom of the vessel as seen by an observer just above the top of the vessel is:
d′=4ln(2) meters
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - RAY OPTICSEXERCISE - PROBLEMS ( LEVEL-I)57videos
RAY OPTICS
- BOOK - AAKASH SERIESCHAPTER - PRACTICAL PHYSICSEXERCISE - LECTURE SHEET LEVEL-II (ADVANCED) Linked Comprehension Type Questions4videos
PRACTICAL PHYSICS
- BOOK - AAKASH SERIESCHAPTER - SEMICONDUCTOR DEVICESEXERCISE - EXERCISE - III3videos
SEMICONDUCTOR DEVICES
Similar Questions
A vessel of depth 2d cm is half filled with a liquid of refractive index μ1 and the upper half with a liquid of refractive index μ2. The apparent depth of the vessel seen perpendicularly is
View SolutionA person looking through a telescope focuses lens at a point on the edge of the bottom of an empty cylindrical vessel. Next he fills the entire vessel with a liquid oif refractive index μ, without disturbing the telescope. Now, he observes the mid point of the vessel. Determine the radius to depth ratio of the vessel
View Solution
Knowledge Check
- Question 1 - Select One
A vesse of depth x is half filled with oil of refractive index μ1 and the other half is filled with water of refrative index μ2. The apparent depth of the vessel when viewed above is
Ax(μ1+μ2)2μ1μ2Bxμ1μ22(μ1+μ2)Cxμ1μ2(μ1+μ2)D2x(μ1+μ2)μ1μ2
A vessel of depth 2h is half filled with a liquid of refractive index 2√2 and the upper half with another liquid of refractive index √2. The liquids are immiscible. The apparent depth of the inner surface of the bottom of vessel will be:
View SolutionA beaker is filled with two immiscible transparent liquids of refractive indices μ1 and μ2 having thickness of layers d1 and d2 respectively. The apparent depth of the bottom of the beaker is
View SolutionA man observes a coin placed at the bottom of a beaker which contains two immiscible liquids of refractive indices 1.2 and 1.4 as shown in the figure. Find the depth of the coin below the surface, as observed from above.
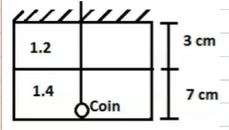 View Solution
View SolutionA concave mirror of radius of curvature h is placed at the bottom of a tank containing a liquid of refractive index μ upto a depth d. An object P is placed at height h above the bottom of the miror. Outside the liquid, an observer O views the object and its image in the mirror. The apparent distance between these two will be
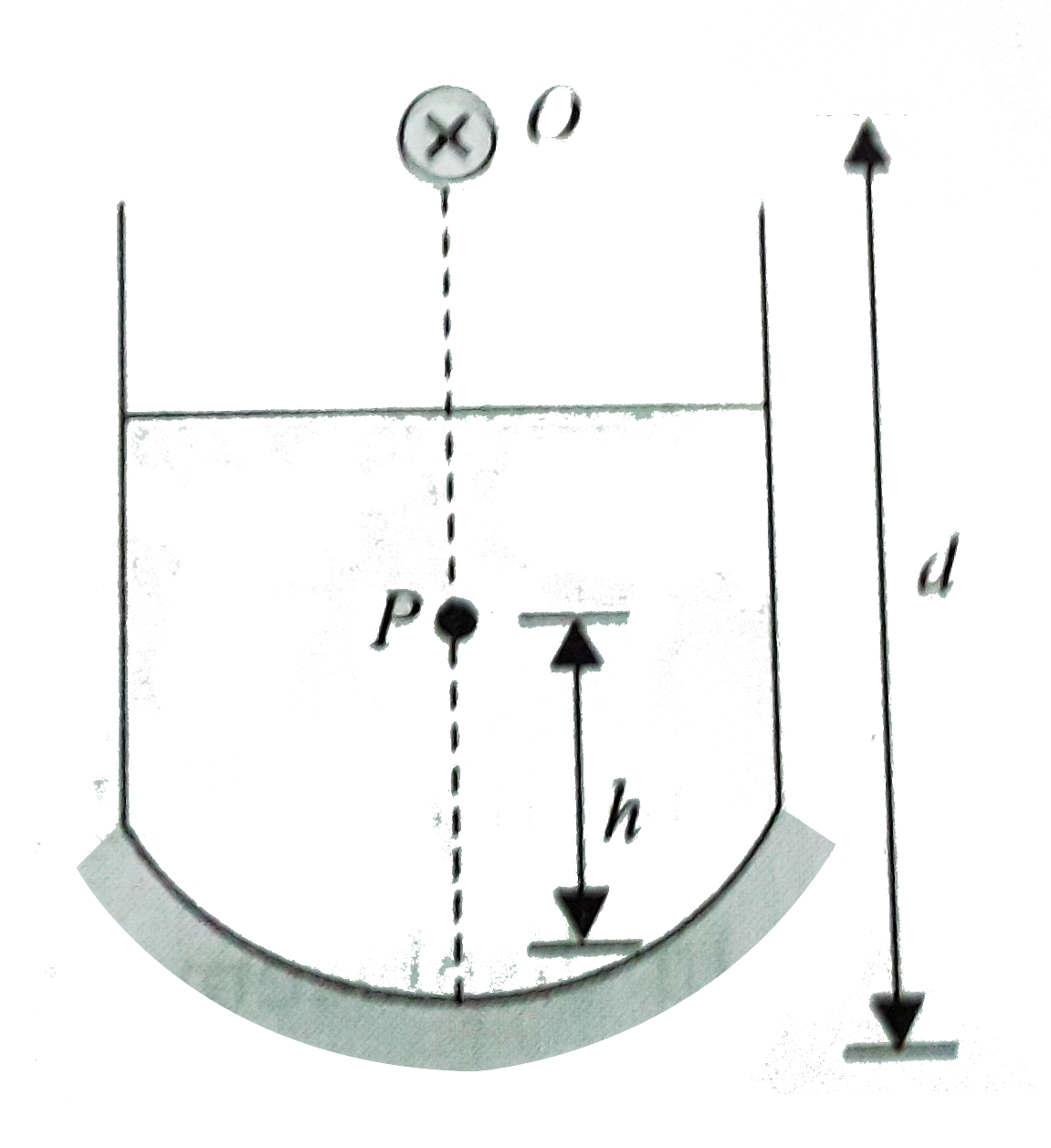 View Solution
View SolutionA small object is placed at the centre of the bottom of a cylindrical vessel of radius 3 cm and height 4 cm filled completely with water. Consider the ray leaving the vessel through a corner. Suppose this ray and the ray along the axis of the vessel are used to trace the image. Find the apparent depth of the image and the ratio of real depth to the apparent depth under the assumptions taken. Refractive index -of water = 1-33.
View SolutionA vessle of depth d is first filled to (23)rd of its depth with a liquid of refractive index 32 and the rest of the vessel is filled with a liquid of refractive index 43. What is the apparent depth of the inner surface of the bottom of the vessle.
View SolutionA vessle of depth d is first filled to (23)rd of its depth with a liquid of refractive index 32 and the rest of the vessel is filled with a liquid of refractive index 43. What is the apparent depth of the inner surface of the bottom of the vessle.
View Solution
