A wire carrying a current i is first bent in the form of a square of side a and placed at right angle to a uniform magnetic field of induction B. The work done in changing its shape' into a circle is
ia2B(π+2)
ia2B(π−2)
ia2B(4π−1)
ia2B(1−4π)
The correct Answer is:C
To solve the problem of calculating the work done in changing the shape of a wire carrying current from a square to a circle while placed in a magnetic field, we can follow these steps:
1. Identify the Initial Shape and Area:
- The wire is initially bent into a square with each side of length a.
- The area of the square, Ainitial, is given by:
Ainitial=a2
2. Determine the Final Shape and Area:
- The wire is reshaped into a circle.
- The circumference of the square is 4a, which will be equal to the circumference of the circle.
- The circumference of the circle is given by 2πr, where r is the radius of the circle.
- Setting these equal gives:
4a=2πr⟹r=2aπ
- The area of the circle, Afinal, is given by:
Afinal=πr2=π(2aπ)2=4a2π
3. Calculate the Work Done:
- The work done in changing the shape of the wire can be calculated using the change in potential energy in the magnetic field.
- The potential energy U in a magnetic field is given by:
U=−iABcos(θ)
- Since the wire is placed at a right angle to the magnetic field, cos(θ)=1.
- Therefore, the initial potential energy Uinitial is:
Uinitial=−iAinitialB=−ia2B
- The final potential energy Ufinal is:
Ufinal=−iAfinalB=−i(4a2π)B
- The work done W is the change in potential energy:
W=Ufinal−Uinitial=(−i4a2πB)−(−ia2B)
- Simplifying this gives:
W=−iB(4a2π−a2)=−iBa2(4π−1)
- Factoring out −iBa2:
W=−iBa2(1−4π)
4. Final Expression for Work Done:
- The work done in changing the shape of the wire from a square to a circle is:
W=ia2B(1−4π)
Conclusion:
The work done in changing the shape of the wire from a square to a circle is:
W=ia2B(1−4π)
- The wire is initially bent into a square with each side of length a.
- The area of the square, Ainitial, is given by:
Ainitial=a2
- The wire is reshaped into a circle.
- The circumference of the square is 4a, which will be equal to the circumference of the circle.
- The circumference of the circle is given by 2πr, where r is the radius of the circle.
- Setting these equal gives:
4a=2πr⟹r=2aπ
- The area of the circle, Afinal, is given by:
Afinal=πr2=π(2aπ)2=4a2π
- The work done in changing the shape of the wire can be calculated using the change in potential energy in the magnetic field.
- The potential energy U in a magnetic field is given by:
U=−iABcos(θ)
- Since the wire is placed at a right angle to the magnetic field, cos(θ)=1.
- Therefore, the initial potential energy Uinitial is:
Uinitial=−iAinitialB=−ia2B
- The final potential energy Ufinal is:
Ufinal=−iAfinalB=−i(4a2π)B
- The work done W is the change in potential energy:
W=Ufinal−Uinitial=(−i4a2πB)−(−ia2B)
- Simplifying this gives:
W=−iB(4a2π−a2)=−iBa2(4π−1)
- Factoring out −iBa2:
W=−iBa2(1−4π)
- The work done in changing the shape of the wire from a square to a circle is:
W=ia2B(1−4π)
The work done in changing the shape of the wire from a square to a circle is:
W=ia2B(1−4π)
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-II
79 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question
15 Videos
- NUCLEAR PHYSICSBOOK - AAKASH SERIESCHAPTER - NUCLEAR PHYSICSEXERCISE - ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED) Integer Type Questions
3 Videos
Similar Questions
A wire carrying current i is bent as shown in figure and placed in the plane of uniform magnetic field Bvec. The magnitude of magnetic force experienced by
View SolutionA wire carrying current l, bent in the form of a quarter circle is held at rest on a smooth table with two threads as shown. A uniform magnetic field exists in the region direction into the plane select the correct alternatives

View SolutionA wire PQR carrying a current l is bent as shown in the figure. It is placed in a uniform magnetic field B. What is the ratio of magnitude of the force on PQ to that on QR ?
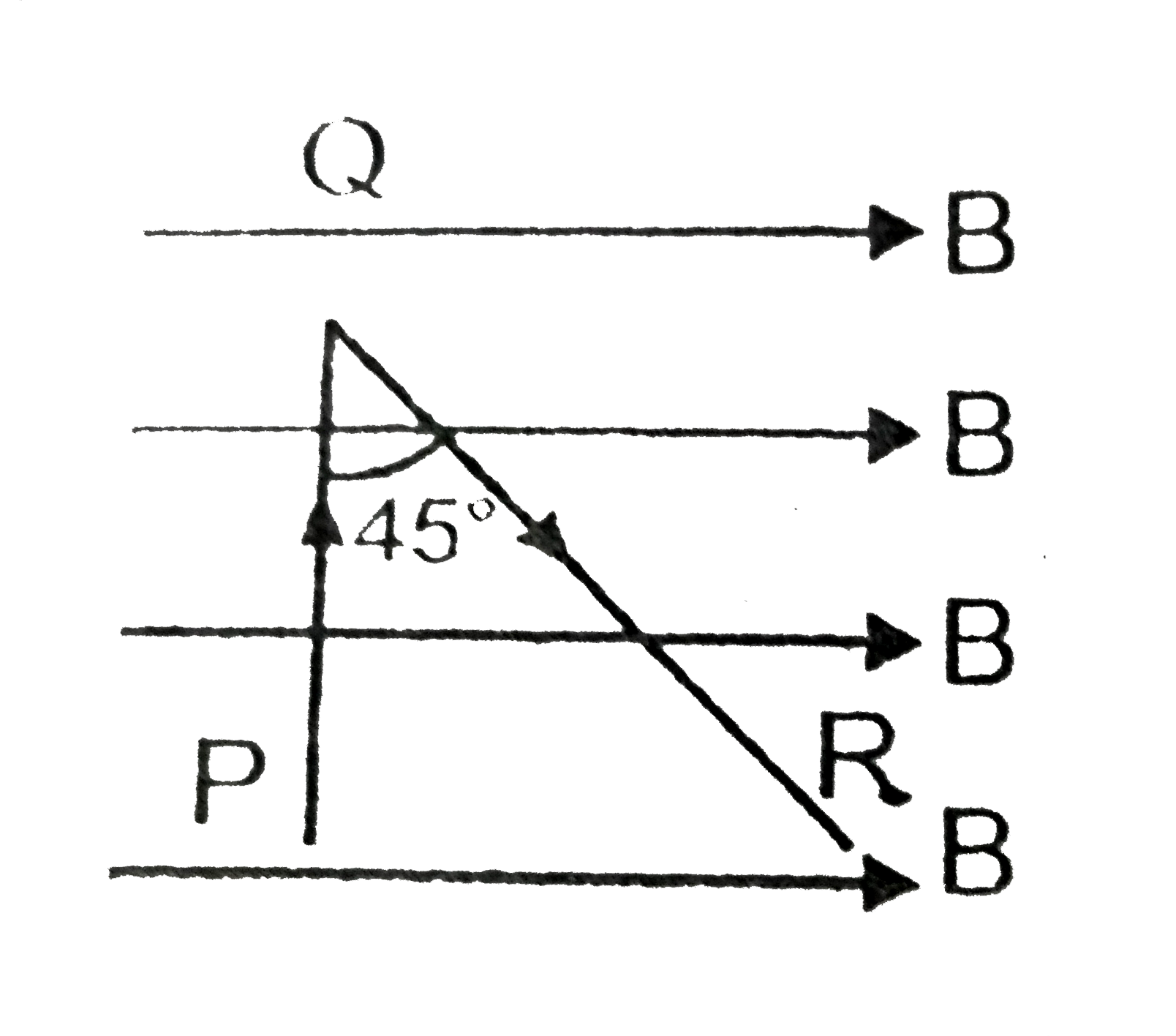
View Solution
A conducting wire MN carrying a current I is bent into the shape as shown and placed in xy plane. A uniform magnetic field →B=−Bˆk is existing in the region. The net magnetic force experenced by the conducting wire MN is
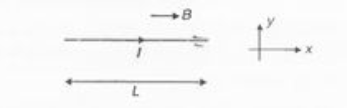
View Solutionthe force on current carrying wire placed in uniform magnetic field B as shown in figure is
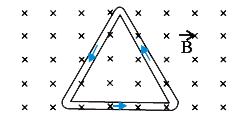
View SolutionA wire is bent in the form of an equilateral triangle of side 1m and carries a current of 2A.. It is placed in a magnetic field of induction 2.0 T directed into the plane of paper. The direction and magnitude of magnetic force acting on each side of the triangle will be
View SolutionA piece of wire carrying a current of 6.00 A is bent in the form of a circular arc of radius 10.0 cm, and it subtends an angle of 120∘ at the centre. Find the magnetic field B due to this piece of wire at the centre.
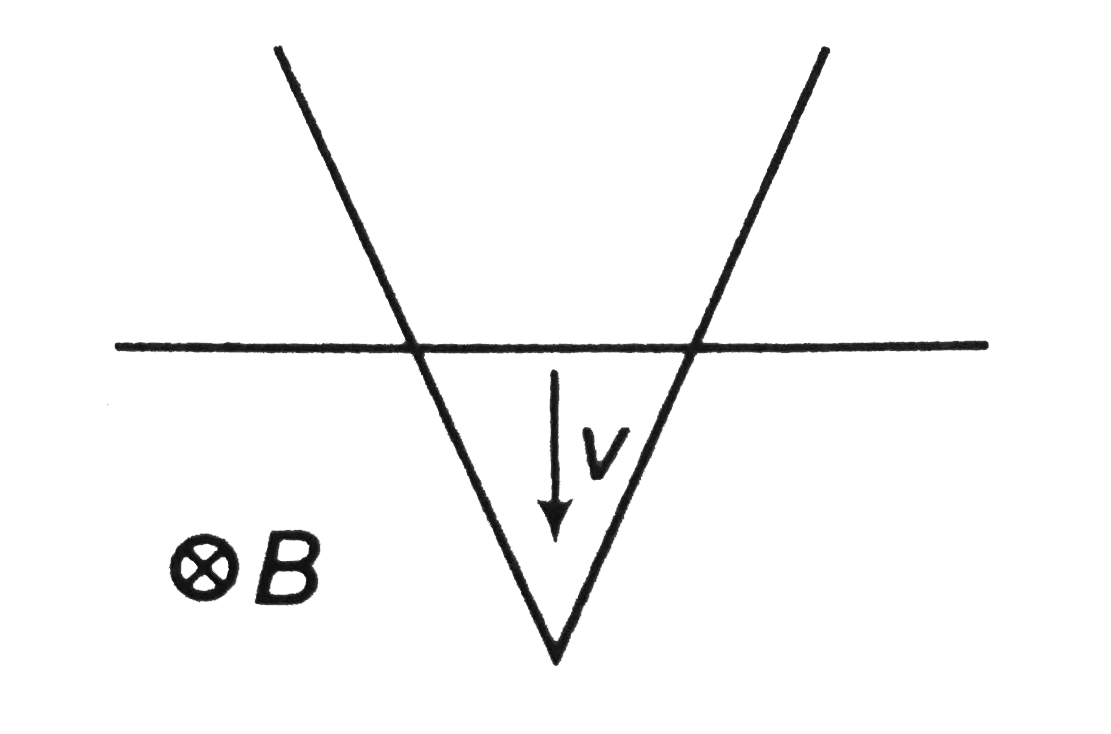
View SolutionA wire is bent in the form of a V shape and placed in a horizontal plane.There exists a uniform magnetic field B perpendicular to the plane of the wire. A uniform conducting rod starts sliding over the V shaped wire with a constant speed v as shown in the figure. If the wire no resistance, the current in rod wil
View SolutionA wires PQRS carrying a current I runs along three edges of a cube of side l as shown in figure. There exists a uniform magnetic field of magnitude B along one of the sides of cube. The magnitude of the force acting on the wire is
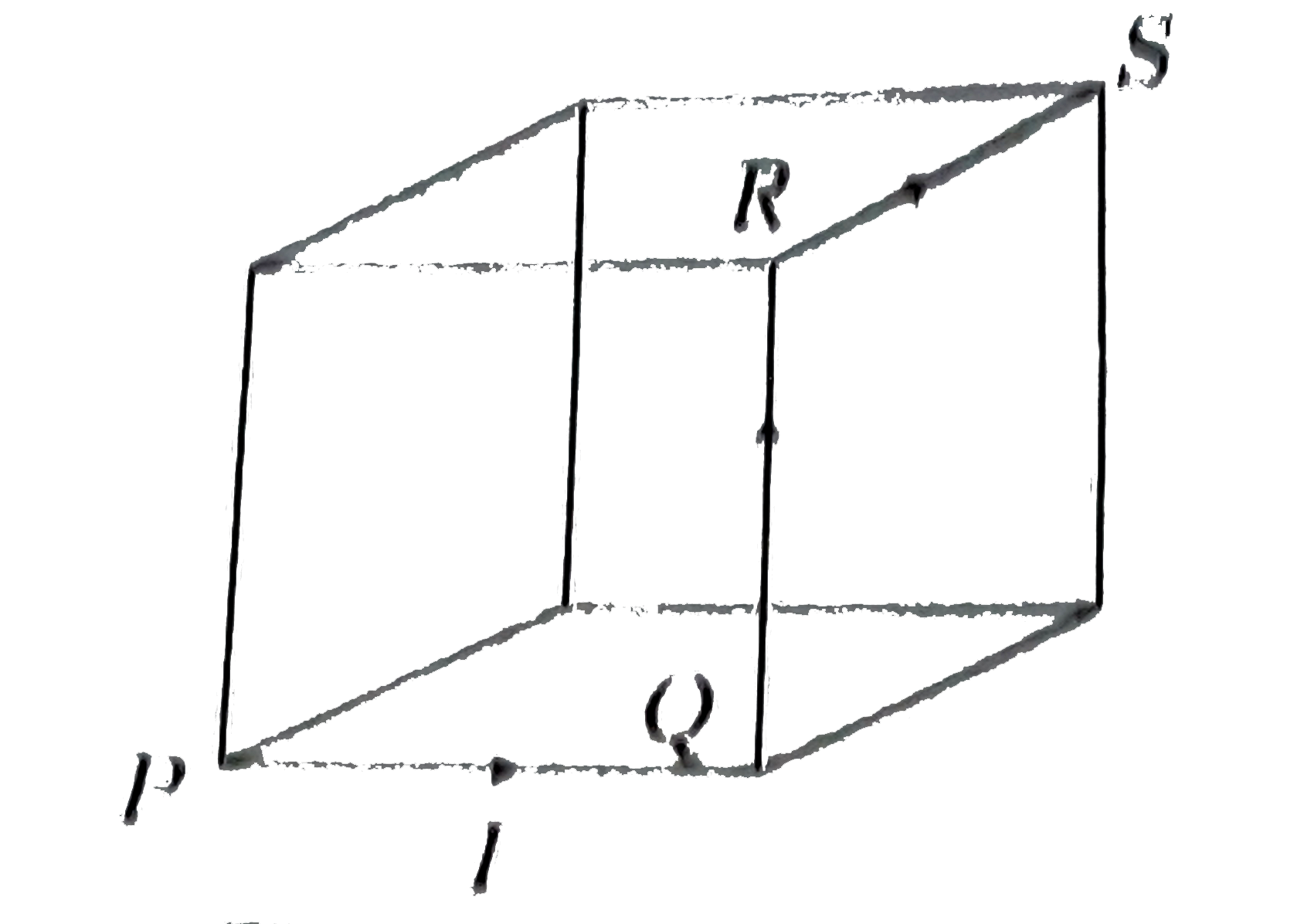
View SolutionA metallic wire is folded to form a square loop a side 'a'. It carries a current 'I' and is kept perpendicular to a uniform magnetic field. If the shape of the loop is changed from square to a circle without changing the length of thw wire and current, the amount of work done in doing so is
View Solution
