Two identical galvanometers are converted into an ammeter and a milliammeter. If the shunt, which has more resistance, the current passing through the coil will be
less
equal
more
zero
The correct Answer is:C
To solve the problem, we need to understand how a galvanometer is converted into an ammeter and a milliammeter using shunt resistors. Here’s a step-by-step solution:
Step 1: Understand the setup
Two identical galvanometers are used, one converted into an ammeter (which measures larger currents) and the other into a milliammeter (which measures smaller currents). A shunt resistor is used in parallel with the galvanometer to allow most of the current to bypass the galvanometer.
Step 2: Define the variables
Let:
- I = total current entering the circuit
- Ig = current through the galvanometer
- Rg = resistance of the galvanometer
- Rs = resistance of the shunt resistor
Step 3: Apply Kirchhoff’s Law
According to Kirchhoff's law, the potential difference across the galvanometer and the shunt resistor must be the same when they are connected in parallel. Therefore, we can write:
Ig⋅Rg=(I−Ig)⋅Rs
Step 4: Analyze the effect of shunt resistance
If the shunt resistor Rs has a very large resistance compared to the galvanometer's resistance Rg, then:
Rs≫Rg
This implies that most of the current I will pass through the galvanometer. As Rs increases, the term (I−Ig) becomes smaller, which means that Ig must increase to keep the equation balanced.
Step 5: Conclude the relationship
Thus, if the shunt resistance Rs is very large, the current passing through the galvanometer Ig will be larger. Therefore, the current passing through the coil (the galvanometer) will increase as the shunt resistance increases.
Final Answer
The current passing through the coil will be more if the shunt resistance is more.
---
Two identical galvanometers are used, one converted into an ammeter (which measures larger currents) and the other into a milliammeter (which measures smaller currents). A shunt resistor is used in parallel with the galvanometer to allow most of the current to bypass the galvanometer.
Let:
- I = total current entering the circuit
- Ig = current through the galvanometer
- Rg = resistance of the galvanometer
- Rs = resistance of the shunt resistor
According to Kirchhoff's law, the potential difference across the galvanometer and the shunt resistor must be the same when they are connected in parallel. Therefore, we can write:
If the shunt resistor Rs has a very large resistance compared to the galvanometer's resistance Rg, then:
Thus, if the shunt resistance Rs is very large, the current passing through the galvanometer Ig will be larger. Therefore, the current passing through the coil (the galvanometer) will increase as the shunt resistance increases.
The current passing through the coil will be more if the shunt resistance is more.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBook:AAKASH SERIESChapter:MOVING CHARGES AND MAGNETISMExercise:EXERCISE-IB
Explore 71 Videos
- MOVING CHARGES AND MAGNETISMBook:AAKASH SERIESChapter:MOVING CHARGES AND MAGNETISMExercise:EXERCISE-II
Explore 79 Videos
- MOVING CHARGES AND MAGNETISMBook:AAKASH SERIESChapter:MOVING CHARGES AND MAGNETISMExercise:EXERCISE-III
Explore 49 Videos
- MOTION IN A STRAIGHT LINE Book:AAKASH SERIESChapter:MOTION IN A STRAIGHT LINE Exercise:very Short answer type question
Explore 15 Videos
- NUCLEAR PHYSICSBook:AAKASH SERIESChapter:NUCLEAR PHYSICSExercise:ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED) Integer Type Questions
Explore 3 Videos
Similar Questions
State how a moving coil galvanometer can be converted into an ammeter.
View SolutionA galvanometer is to be converted into an ammeter or voltmeter. In which of the following cases the resistance of the device is largest?
View SolutionA galvanometer is to be converted into an ammeter or voltmeter. In which of the following cases the resistance of the device is largest?
View Solution(A) : If a galvanometer is converted into an ammeter and a milliammeter then the shunt resistance of ammeter is lower than that of milliammeter.
(R) : In Ammeter the current through shunt is less than that of galvonameter as compared to the case of milliammeter.
View SolutionA moving coil galvnometer is converted into an ammeter reading up to 0.03A by connecting a shunt of resistance r4. What is the maximum current which can be sent through this galvanometer if no shunt is used (here r=resistance of galvanometer)
View SolutionAn ammeter and a milliammeter are converted from identical galvanometers. Which one has smaller resistance ?
View Solution(a) Briefly explain how a galvanometer is converted into an ammeter.
(b) A galvanometer coil has a resistance of 15Ω and it shows full scale deflection for a current of 4 mA. Convert it into an ammeter of range 0 to 6 A.
View SolutionIn the given circuit, a galvanometer with a resistance of 70Ω is converted to an ammeter 0.05Ω by a shunt resistance of 0.052, total current measured by this device
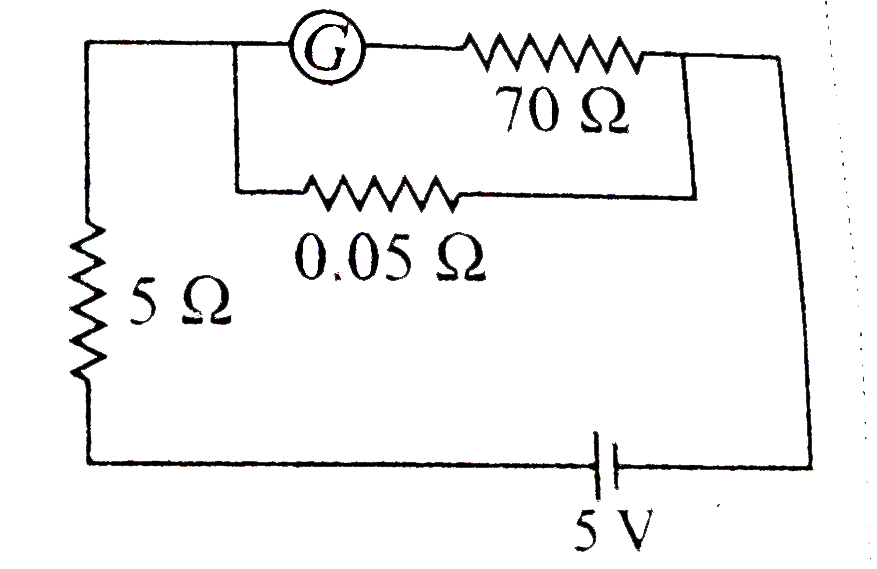
View SolutionA galvanometer having a resistance of 8 ohm is shunted by a wire of resistance 2 ohm . If the total current is 1 amp , the part of it passing through the shunt will be
View SolutionA galvanometer having a resistance of 8 ohm is shunted by a wire of resistance 2 ohm . If the total current is 1 amp , the part of it passing through the shunt will be
View Solution

