Two identical long conducting wires AOB and COD are placed at right angle to each other, with one above other such that O is their common point for the two. The wires carry l1 and l2 currents, respectively. Point P is lying at distance d from 0 along a direction perpendicular to the plane containing the wire. The magnetic field at the point P will be
μ02πd(I1I2)
μ02πd(I1+I2)
μ02πd(I21+I22)
μ02πd(I21+I22)1/2
The correct Answer is:D
To find the magnetic field at point P due to the two perpendicular conducting wires carrying currents I1 and I2, we can follow these steps:
Step 1: Understand the Configuration
We have two long, straight, identical conducting wires AOB and COD placed at right angles to each other. The currents in the wires are I1 (in wire AOB) and I2 (in wire COD). The point P is located at a distance d from the common point O, perpendicular to the plane formed by the wires.
Step 2: Magnetic Field Due to a Long Straight Wire
The magnetic field B at a distance r from a long straight wire carrying current I is given by the formula:
B=μ0I2πr
where μ0 is the permeability of free space.
Step 3: Calculate the Magnetic Field at Point P
1. Magnetic Field due to Wire AOB (current I1):
- The distance from wire AOB to point P is d.
- The direction of the magnetic field due to wire AOB at point P is given by the right-hand rule. If the current I1 is flowing upwards, the magnetic field at point P will be in the positive y-direction (J cap).
- Therefore, the magnetic field B1 at point P due to wire AOB is:
B1=μ0I12πd^j
2. Magnetic Field due to Wire COD (current I2):
- The distance from wire COD to point P is also d.
- If the current I2 is flowing towards the observer (out of the plane), the magnetic field at point P will be in the negative x-direction (−I cap).
- Therefore, the magnetic field B2 at point P due to wire COD is:
B2=−μ0I22πd^i
Step 4: Find the Net Magnetic Field
The net magnetic field Bnet at point P is the vector sum of B1 and B2:
Bnet=B1+B2=μ0I12πd^j−μ0I22πd^i
Step 5: Calculate the Magnitude of the Net Magnetic Field
To find the magnitude of the net magnetic field |Bnet|:
|Bnet|=√(μ0I12πd)2+(−μ0I22πd)2
=μ02πd√I21+I22
Final Answer
Thus, the magnetic field at point P is:
|Bnet|=μ02πd√I21+I22
We have two long, straight, identical conducting wires AOB and COD placed at right angles to each other. The currents in the wires are I1 (in wire AOB) and I2 (in wire COD). The point P is located at a distance d from the common point O, perpendicular to the plane formed by the wires.
The magnetic field B at a distance r from a long straight wire carrying current I is given by the formula:
B=μ0I2πr
where μ0 is the permeability of free space.
1. Magnetic Field due to Wire AOB (current I1):
- The distance from wire AOB to point P is d.
- The direction of the magnetic field due to wire AOB at point P is given by the right-hand rule. If the current I1 is flowing upwards, the magnetic field at point P will be in the positive y-direction (J cap).
- Therefore, the magnetic field B1 at point P due to wire AOB is:
B1=μ0I12πd^j
- The distance from wire COD to point P is also d.
- If the current I2 is flowing towards the observer (out of the plane), the magnetic field at point P will be in the negative x-direction (−I cap).
- Therefore, the magnetic field B2 at point P due to wire COD is:
B2=−μ0I22πd^i
The net magnetic field Bnet at point P is the vector sum of B1 and B2:
Bnet=B1+B2=μ0I12πd^j−μ0I22πd^i
To find the magnitude of the net magnetic field |Bnet|:
|Bnet|=√(μ0I12πd)2+(−μ0I22πd)2
=μ02πd√I21+I22
Thus, the magnetic field at point P is:
|Bnet|=μ02πd√I21+I22
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBook:AAKASH SERIESChapter:MOVING CHARGES AND MAGNETISMExercise:EXERCISE-IB
Explore 71 Videos
- MOVING CHARGES AND MAGNETISMBook:AAKASH SERIESChapter:MOVING CHARGES AND MAGNETISMExercise:EXERCISE-II
Explore 79 Videos
- MOVING CHARGES AND MAGNETISMBook:AAKASH SERIESChapter:MOVING CHARGES AND MAGNETISMExercise:EXERCISE-III
Explore 49 Videos
- MOTION IN A STRAIGHT LINE Book:AAKASH SERIESChapter:MOTION IN A STRAIGHT LINE Exercise:very Short answer type question
Explore 15 Videos
- NUCLEAR PHYSICSBook:AAKASH SERIESChapter:NUCLEAR PHYSICSExercise:ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED) Integer Type Questions
Explore 3 Videos
Similar Questions
Two identical conducting wires AOBandCOD are placed at right angles to each other. The wire AOB carries an electric current I1andCOD carries a current I2. The magnetic field on a point lying at a distance d from O, in a direction perpendicular to the plane of the wires AOBandCOD, will be given by
View SolutionA conducting wire carrying current I is shown in the figure. The magnitude of magnetic field at the point P will be

View SolutionTwo perpendicular infinite wires are carrying current i as shown in the figure. The magnetic field at point P is :
_2019_CBT2_E01_008_Q01.png)
View SolutionA wire of infinite length bent as shown in figure carries current l. What is the magnetic field at the point P ?

View SolutionThe straight long conductors AOB and COD are perpendicular to each other and carry current i1 and i2. The magnitude of the magnetic induction at point P at a distance a from the point O in a direction perpendicular to the plane ACBD is
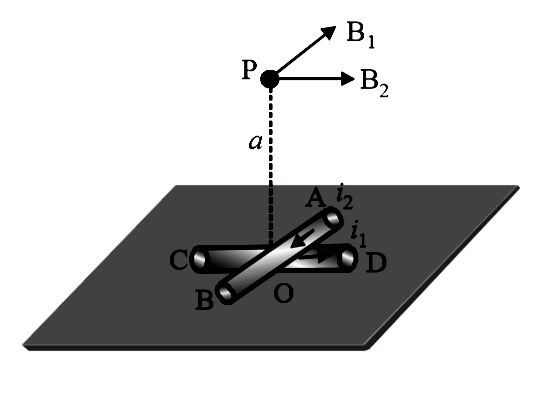
View SolutionThe straight long conductors AOB and COD are perpendicular to each other and carry current i1 and i2. The magnitude of the magnetic induction at point P at a distance a from the point O in a direction perpendicular to the plane ACBD is

View SolutionTwo long parallel wires carry equal current I flowing in the same direction are at a distance 2d apart. The magnetic field B at a point lying on the perpendicular line joining the wires and at a distance x from the midpoint is
View SolutionWhen two parallel wires carrying current l and 2l in same direction are placed at a distance d apart, the ratio of force per unit length acting upon the wire due to other is
View SolutionA point charge +q is placed at a distance d from an isolated conducting plane. The field at a point P on the other side of plane is
View SolutionA point charge +q is placed at a distance d from an isolated conducting plane. The field at a point P on the other side of plane is
View Solution

