Following are four different relations about displacement, velocity and acceleration for the motion of a particle in general. Choose the incorrect one (s).
(a)vav=12[v(t1)+v(t2)]
(b)vav=r(t2)−r(t1)t2−t1
(c)r=12(v(t2)−v(t1))(t2−t1)
(d)aav=v(t2)−v(t1)t2−t1
a and b
a and d
b and c
a and c
The correct Answer is:D
Step by step video solution for Following are four different relations about displacement, velocity and acceleration for the motion of a particle in general. Choose the incorrect one (s). (a)v_(av)=1/2[v(t_1)+v(t_2)] (b)v_(av)=(r(t_2)-r(t_1))/(t_2-t_1) (c)r=1/2 (v(t_2)-v(t_1))(t_2-t_1) (d)a_(av)=(v(t_2)-v(t_1))/(t_2-t_1) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
Following are four different relation about displacement,velocity and acceleration for the motion of a particle in general.Choose the incorrect one (S).
a) Vav=12[v(t1)+v(t2)]
b)Vav=r(t2)−r(t2)t2−t1
c)r=12(v(t2)−v(t1)(t2−t1)
d)aav=v(t2)−v(t1)t2−t1
View SolutionVelocity of a particle at any time t is v=(2ˆi+2tˆj)m/s. Find acceleration and displacement of particle at t=1s. Can we apply v=u+at or not?
View Solution
Knowledge Check
For any arbitrary motion in space, which of the following relations are true?
a) vaverage=(1/2)(v(t1+v(t2)
b) vaverage=[r(t2)−rt1t2−t1
v(t)=v(0)+at
d) aaverage=[v(t2)−vt1t2−t1
The average stands for average of the quantity over time interval t1 to t_(2)A→vaverage=12[→v(t1)+→v(t2)]B→vaverage=→r(t2)−→r(t1)t2−t1C→v(t)=→v(0)+→atD→r(t)=→r(0)+→v(0)t+12→at2Two different adiabatic parts for the same gas intersect two isothermals at T1andT_2 as shown in P-V diagram . Then the ratio of VaVb will be
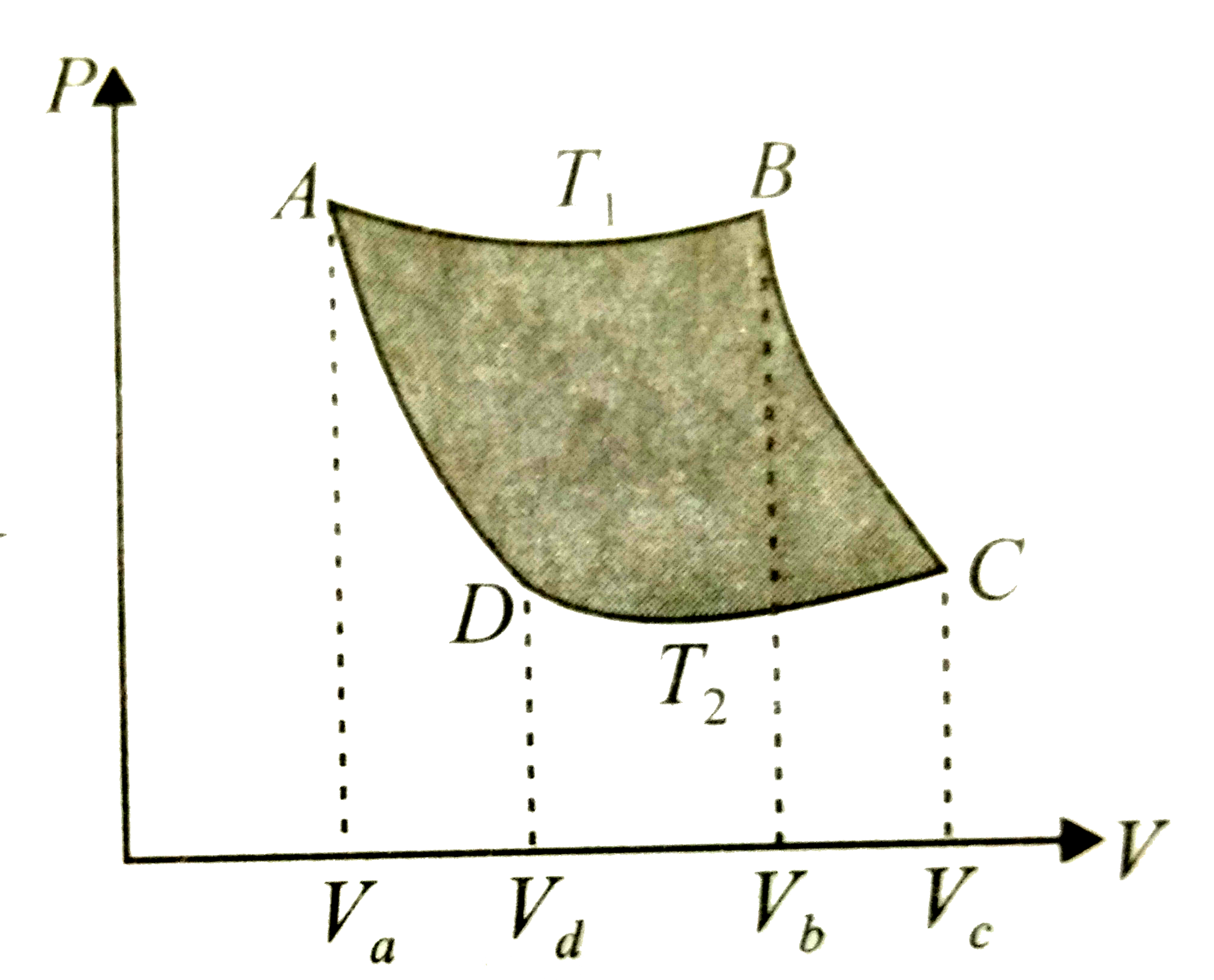 Aa. VcVdBb. VdVcCc. γVdVcDd. 1γVdVc
Aa. VcVdBb. VdVcCc. γVdVcDd. 1γVdVc
Velocity of a particle varies with time as v=4t. Calculate the displacement of particle between t=2 to t=4 sec.
View SolutionThe normal drawn at a point (at21,−2at1) of the parabola y2=4ax meets it again in the point (at22,2at2), then t2=t1+2t1 (b) t2=t1−2t1 t2=−t1+2t1 (d) t2=−t1−2t1
View SolutionVelocity (in m/s) of a particle moving in a straight line given by v=(t2−2t1). Match Table-1 with Table -2
View SolutionWhich among the following relations is correct?
(a)t3/4=2t1/2
(b)t3/4=3t1/2
(c)t3/4=12t1/2
(d)t3/4=13t1/2
View SolutionIf force (F), velocity (V) and time (T) are taken as fundamental units, then the dimensions of mass are
(a)[FvT−1] (b)[FvT−2] (c)[Fv−1T−1] (d)[Fv−1T]
View SolutionIf v=(t2−4t+105)m/s where t is in second. Find acceleration at t=1 sec.
View Solution
