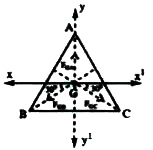
Three equal masses of m kg each are fixed at the vertices of an equilateral triangle ABC.
(a) What is the force acting on a mass 2m placed at the centroid G of the triangle?
(b) What is the force if the mass at the vertex A is doubled?
Take AG=BG=CG=1m (see Fig.8.5)
The individual force in vector notation are
FGA=G(m)(2m)1ˆj
FGB=G(m)(2m)1(−ˆlcos30∘−ˆjsin30∘)
FGC=G(m)(2m)1=(ˆl=cos30∘−ˆjsin30∘)
From the principle of superposition and the law of vector addition the resultant gravitational force FR on (2m) is
FR=FGA+FGB+FGC
FR=2Gm2ˆj+2Gm2(−ˆicos30∘−ˆjsin30∘)
+2Gm2(ˆicos30∘−ˆjsin30∘)=0
(b) By symmetry, the X-component of the force cancels out. The Y-component survives.
∴FR=4Gm2ˆj−2Gm2ˆj=2Gm2ˆj
Similar Questions
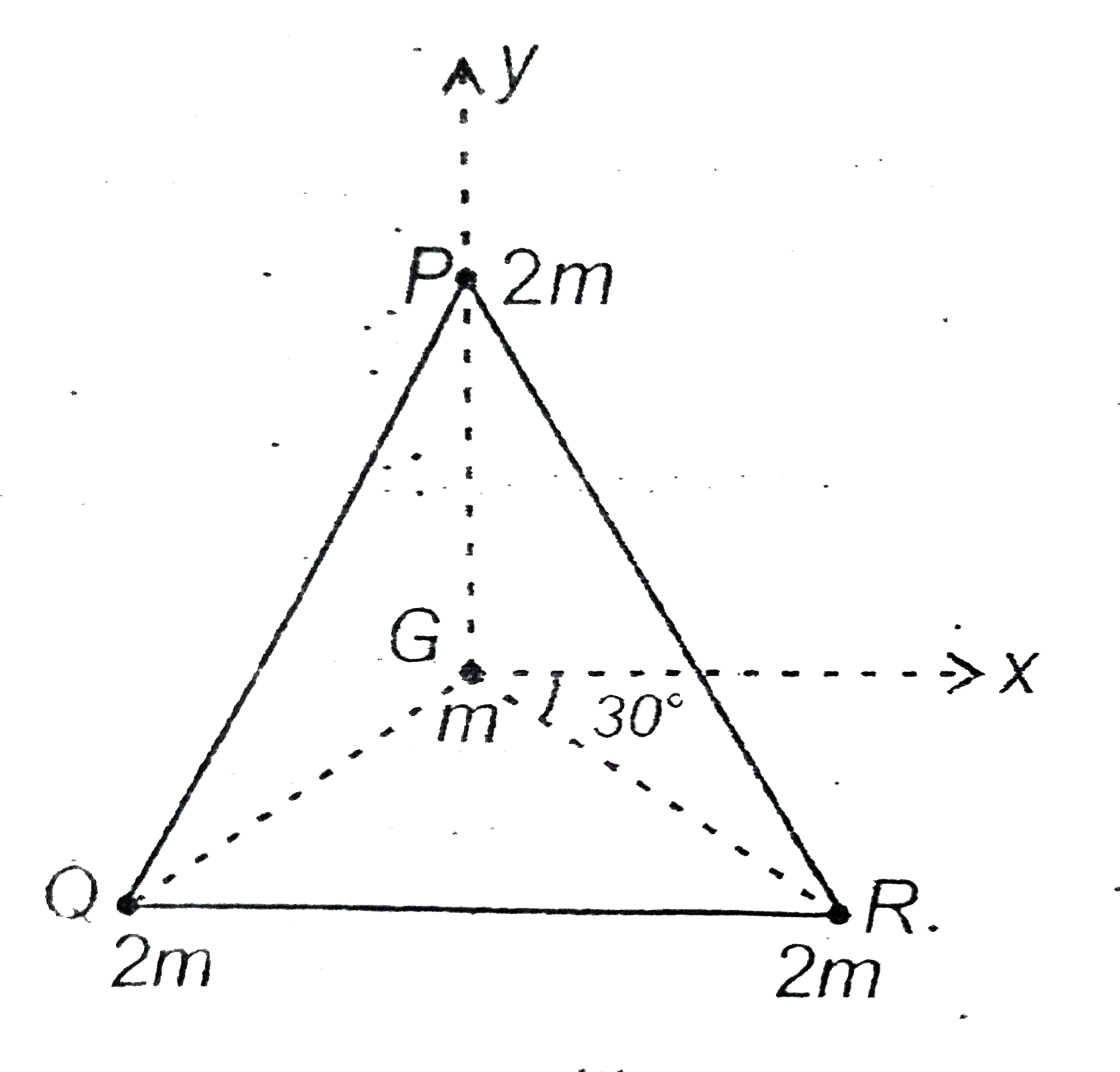
Three equal masses 2m each are placed at the vertices an equilateral triangle PQR
(i) What is the force acting on a mass m placed at the centroid G of the triangle ?
(ii) What is the force on mass m if the mass at the vertex P is quadrupled ?
Take PG = QG = RG = 1m
View SolutionThree equal masses of 1.5 kg each are fixed at the vertices of an equilateral triangle of side 1 m. What is the force acting on a particle of mass 1 kg placed at its centroid ?
View Solution
Knowledge Check
Three masses each of mass m are palced at the vertices of an equilateral triangles ABC of side l as shown in figure. The force acting on a mass 2m placed at the centroid O of the triangle is
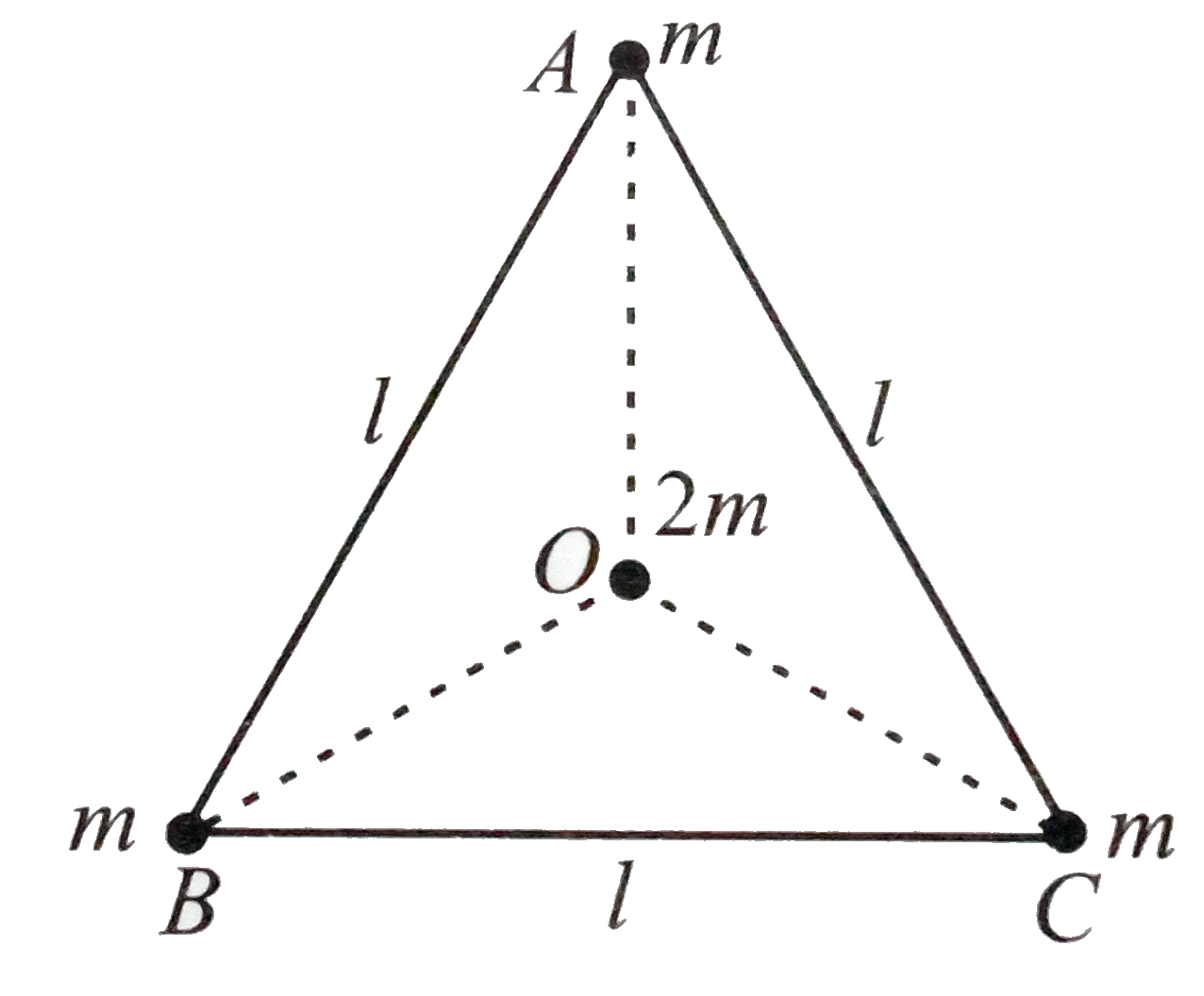 AzeroB3Gm2l2C5Gm2l2D7Gm2l2
AzeroB3Gm2l2C5Gm2l2D7Gm2l2Consider three charges q1,q2 and q3 each equal to q, at the vertices of an equilateral triangle of side l. What is the force on a charge Q placed at the centroid of the triangle?
A3Qq4πε0l2B2Qq4πε0l2CQq2πε0l2Dzero
Three masses of 1 kg each are kept at the vertices of an equilateral triangle of side 3 m. What is the force acting on a point mass of 5 kg placed at its centroid ?
View SolutionThree charges of equal magnitude q is placed at the vertices of an equilateral triangle of side l. The force on a charge Q placed at the centroid of the triangle is
View SolutionThree equal masses of 1 kg each are placed at the vertices of an equilateral triangle of side 1 m, then the gravitational force on one of the masses due to other masses is (approx.)
View SolutionThree equal masses each of mass 'm' are placed at the three-corner of an equilateral triangle of side 'a'
If a fourth particle of equal mass is placed at the centre of triangle, then net force acting on it, is equal to
View SolutionThree mass points each of mass m are placed at the vertices of an equilateral tringale of side l. What is the gravitational field and potential due to three masses at the centroid of the triangle ?
View SolutionThree equal masses of 2kg each are placed at the vertices of an equilateral triangle and a mass of 4 kg is placed at the centroid of the triangle which is at a distance of √2 m from each of the vertices of the triangle. The force, (in newton) acting on the mass of 4 kg is
View Solution
