किसी समबाहु त्रिभुज ABC के प्रत्येक शीर्ष पर m kg के तीन समान द्रव्यमान रखे हैं।
(a) इस त्रिभुज के केन्द्रक G पर रखे 2m kg के द्रव्यमान पर कितना बल आरोपित हो रहा है?
(b)यदि शीर्ष A पर रखे द्रव्यमान को दोगुना कर दिया जाये, | तो कितना बल आरोपित होगा? AG = BG = CG = 1 m लीजिए। (देखिए चित्र)

Video Solution

Text Solution

Verified by Experts

चित्र में किसी समबाहु त्रिभुज ABC के प्रत्येक शीर्ष पर m kg, के तीन समान द्रव्यमान रखे हैं। इसके केन्द्रक G पर कोई द्रव्यमान (2m) रखा गया है।

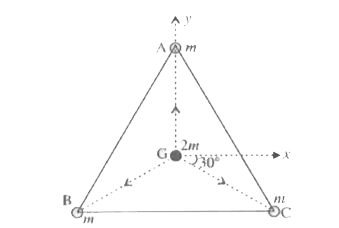
(a) धनात्मक-अक्ष तथा GC के बीच का कोण 30° है।और इतना ही कोण ऋणात्मक x अक्ष तक GB के बीच बनता है
बिन्दु A पर स्थित m द्रव्यमान के कारण बिन्दु G पर स्थित (2m) द्रव्यमान पर कार्यरत बल
${\to F}_{G A} = \frac{G (m) (2 m)}{{(A G)}^{2}} G A$ के अनुदिश $> {\to F}_{G A} = \frac{2 G m^{2}}{1} j$
बिन्दु B पर स्थित m द्रव्यमान के कारण बिन्दु G पर स्थित | (2m) द्रव्यमान पर कार्यरत बल
${\to F}_{G B} = \frac{G (m) (2 m)}{B G} B G$ के अनुदिश,
${\to F}_{G B} = \frac{2 G m^{2}}{1} (i C 0 s 30 ° j sin 30 °)$ बिन्दु C पर स्थित m द्रव्यमान के कारण बिन्दु G पर स्थित 2m द्रव्यमान पर कार्यरत बल
${\to F}_{G C} = {\frac{G (m) (2 m)}{C G}}^{2}) G C$ के अनुदिश
$\Rightarrow \to F (G C) = \frac{2 G m^{2}}{1} (i C 0 s 30 ° - j sin 30 °)$
अध्यारोपण सिद्धान्त तथा सदिश योग नियम के अनुसार (2m) पर परिणामी गुरुत्वाकर्षण
बल ${\to F}_{R} = {\to F}_{G A} + {\to F}_{G B} + {\to F}_{G C}$
${\to F}_{R} = 2 G M^{2} ˆ j + 2 G M^{2} (- i C 0 s ° 30 - ˆ j sin ° 30)$
$+ 2 G M^{2} (i C 0 s ° 30 - j sin ° 30)$
$= 2 G M^{2} (ˆ j - i C 0 s ° 30 - ˆ j sin ° 30 + i C 0 s ° 30 - ˆ j sin 30 °)$
$= 2 G M^{2} (ˆ j - ˆ j) = 0$
अतः त्रिभुज के केन्द्रक पर शून्य बल आरोपित हो रहा है।(b) अब यदि बिन्दु A पर स्थित द्रव्यमान को दुगुना अर्थात् (2m) कर दिया जाये तब
${\to F}_{G A} = \frac{G (2 m) (2 m)}{1} ˆ j$
$\frac{4 G m^{2}}{1} ˆ j$
जबकि ${\to F}_{G B}$ तथा $\to F (G C)$ अपरिवर्तित रहेंगे।
$∴ {\to F}_{R} = {\to F}_{G A} + {\to F}_{G B} + {\to F}_{G C}$
$= 4 G m^{2} ˆ j + 2 G m^{2} (- i C 0 s 30 ° - ˆ j sin 30 °)$
$+ 2 G m^{2} (ˆ i C 0 s 30 ° - - ˆ j sin 30 °)$
$= 26 m^{2} (2 ˆ j - ˆ i C 0 s 30 ° - ˆ j sin 30 °$ +
$ˆ i C 0 s 30 ° - ˆ j sin 30 °)$
$= 26 m^{2} (2 ˆ j - 2 ˆ j sin 30 °) = 2 G m^{2} (2 ˆ j - ˆ j)$ 2Gm^(2)hatj Ans.

Updated on:21/07/2023

|

Class 11 PHYSICS GRAVITATION

Topper's Solved these Questions

Similar Questions

SANJEEV PUBLICATION-गुरुत्वाकर्षण (Gravitation)-गत वर्षों की विभिन्न प्रतियोगी परीक्षाओं में पूछे गये प्रश्न

Home
Ask Doubt
Profile