A conical pendulum of length 1 m makes an angle θ=45∘ w.rt Z-axis and moves in a circle in the XY plane. The radius of the circle is 0.4 m and its center is vertically below O. The speed of the pendulum, in its circular path, will be : (Take g=10ms−2)

0.4 m/s
2m/s
0.2 m/s
4m/s
The correct Answer is:B
Step by step video solution for A conical pendulum of length 1 m makes an angle theta = 45^@ w.rt Z-axis and moves in a circle in the XY plane. The radius of the circle is 0.4 m and its center is vertically below O. The speed of the pendulum, in its circular path, will be : (Take g=10ms^(-2)) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
A particle of mass 200 g is moving in a circle of radius 2 m. The particle is just looping the loop. The speed of the particle and the tension in the string at highest point of the circule path are (g=10ms−2)
View SolutionA particle of mass 200 g is moving in a circle of radius 2 m. The particle is just looping the loop. The speed of the particle and the tension in the string at highest point of the circule path are (g=10ms−2)
View SolutionA particle is moving on a circular path of radius 10m with uniform speed of 4ms−1.The magnitude of change in velocity of particle when it completes a semi circular path is
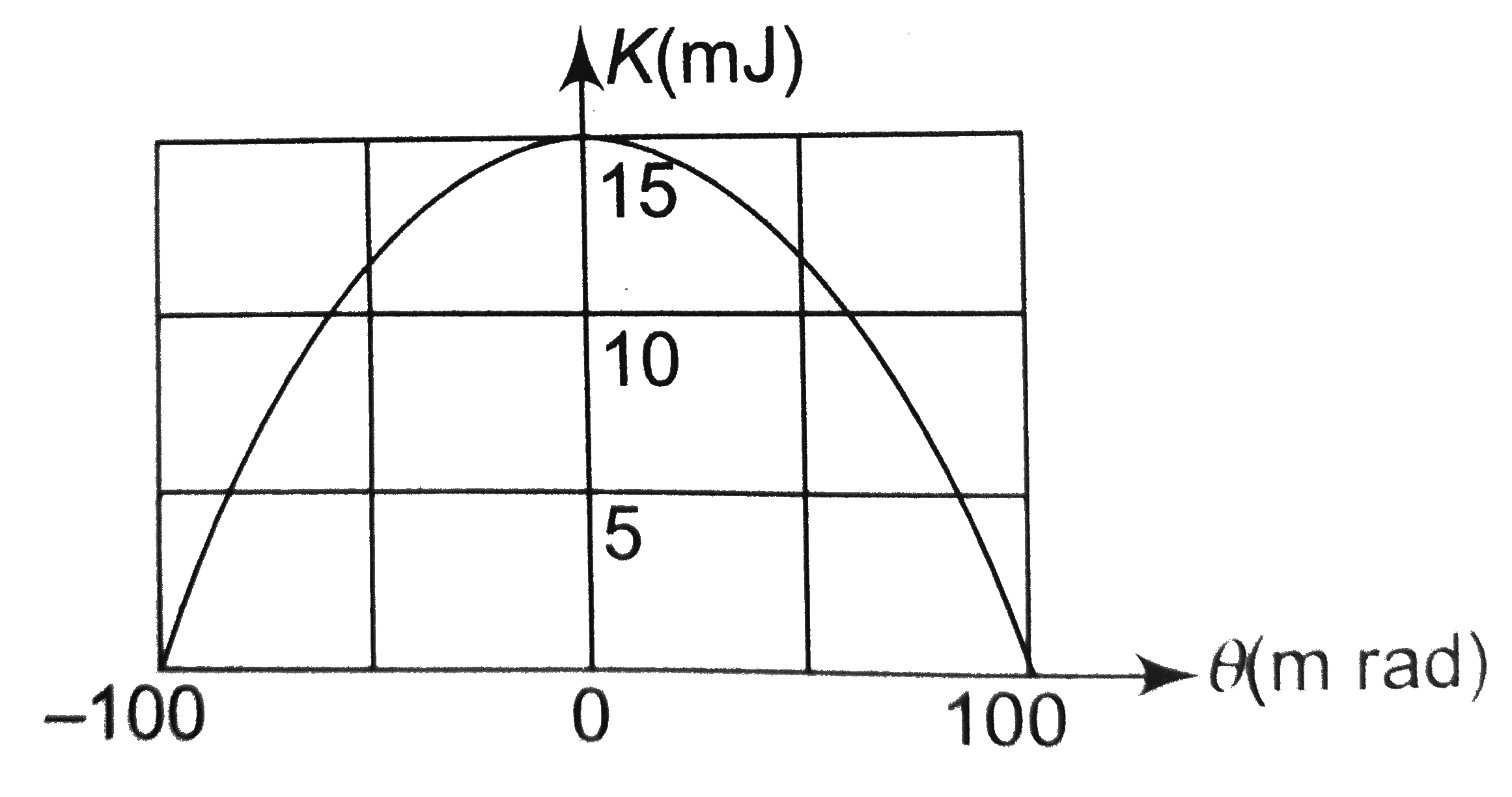
View SolutionFigure shown the kinetic energy K of a pendulum versus. its angle θ from the vertical. The pendulum bob has mass 0.2kg The length of the pendulum is equal to (g=10m/s2)
,
View SolutionA mark on the rim of a rotating cicular wheel of 0.50 m radius is moving with a speed of 10ms−1 . Find its angular speed.
View SolutionA stone of 1 kg tied up with 10/3 m long string rotated in a vertical circle. If the ratio of maximum and minimum tension in string is 4 then speed of stone at highest point of circular path will be ( g=10ms2)
View SolutionThe bob of a simple pendulum of length 1 m has mass 100 g and a speed of 1.4 m/s at the lowest point in its path. Find the tension in the stirng at this instant.
View SolutionIn a conical pendulum a small mass is revolving in horizontal circle with constant speed v at the end of the cord of length L that makes an angle θ with the vertical as shown . The value of angle θ would be (where r is the radius of circle)

View SolutionFig. show a conical pendulum. If the length of the pendulum is l, mass of die bob is m and θ is the angle made by the string with the vertical show that the angular momentum of the pendulum about the point of support is:
L=√m2gl3sin4θcosθ
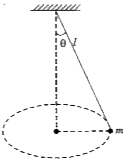
View SolutionA simple pendulum of length 1m is allowed to oscillate with amplitude 2∘. it collides at T to the vertical its time period will be (use g=π2)
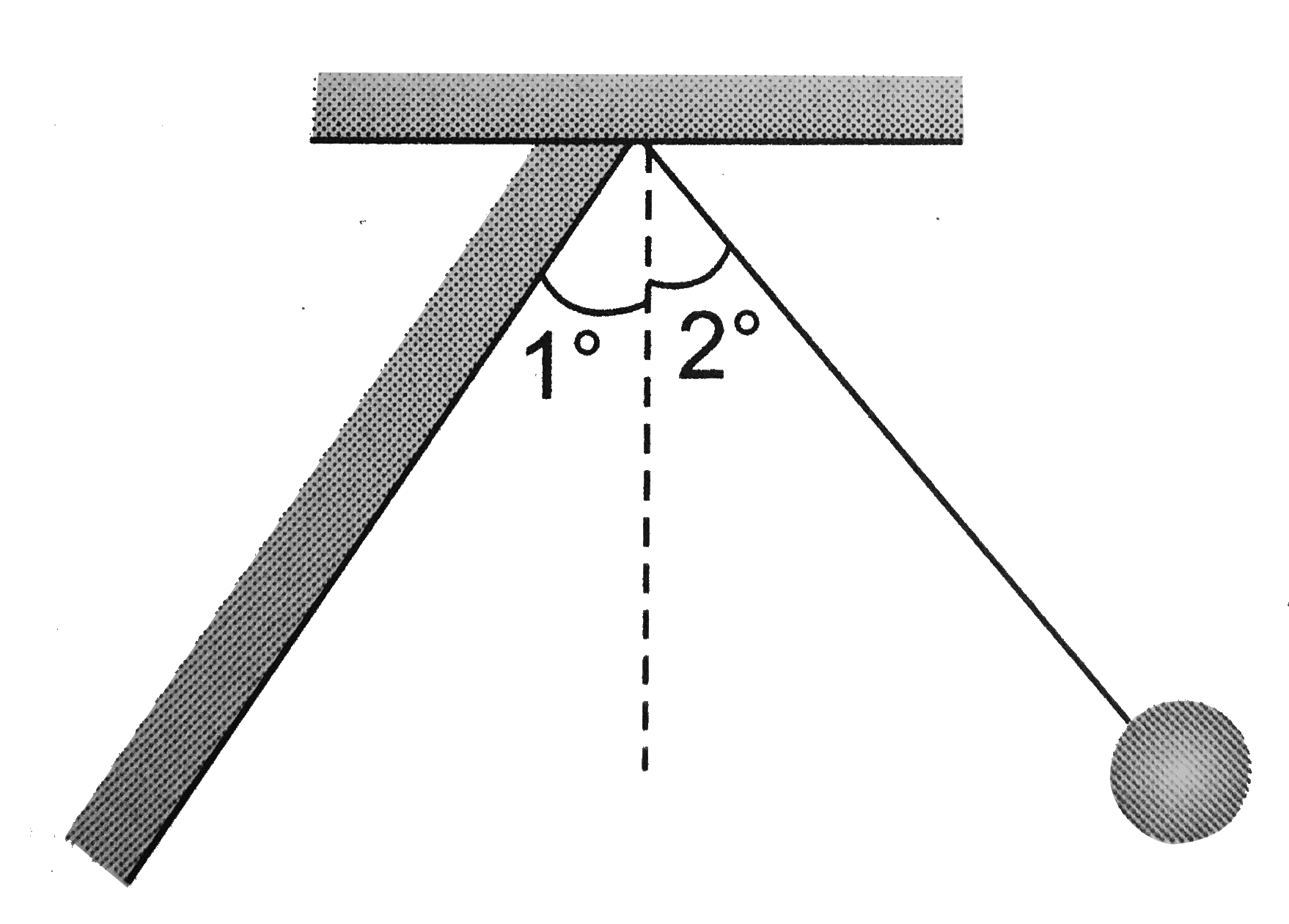
View Solution