A conical pendulum of length L makes an angle θ with the vertical. The time period will be

2π√lcosθg
2π√Lgcosθ
2π√Ltanθγ
2π√Lgtanθ
The correct Answer is:A
Tcosθ=mg,Tsinθ=mRω2
or tanθ=Rω2g=R(2π/T)2g
T=2π√Rgtanθ
But R=Lsinθ
∴ T=2π√Lcosθg
Topper's Solved these Questions
- CIRCULAR MOTIONBook:DC PANDEYChapter:CIRCULAR MOTIONExercise:Match the columns
Explore 3 Videos
- CIRCULAR MOTIONBook:DC PANDEYChapter:CIRCULAR MOTIONExercise:Medical entrances s gallery
Explore 19 Videos
- CIRCULAR MOTIONBook:DC PANDEYChapter:CIRCULAR MOTIONExercise:Check point
Explore 45 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEYChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 2 Subjective
Explore 21 Videos
- COMMUNICATION SYSTEMBook:DC PANDEYChapter:COMMUNICATION SYSTEMExercise:Only One Option is Correct
Explore 27 Videos
Similar Questions
A charged particle having its charge to mass ratio as β goes in a conical pendulum oflength L making an angle θ with vertical and angular velocity ω. If a magnetic field B is directed vertically downwards (see figure-4.238):
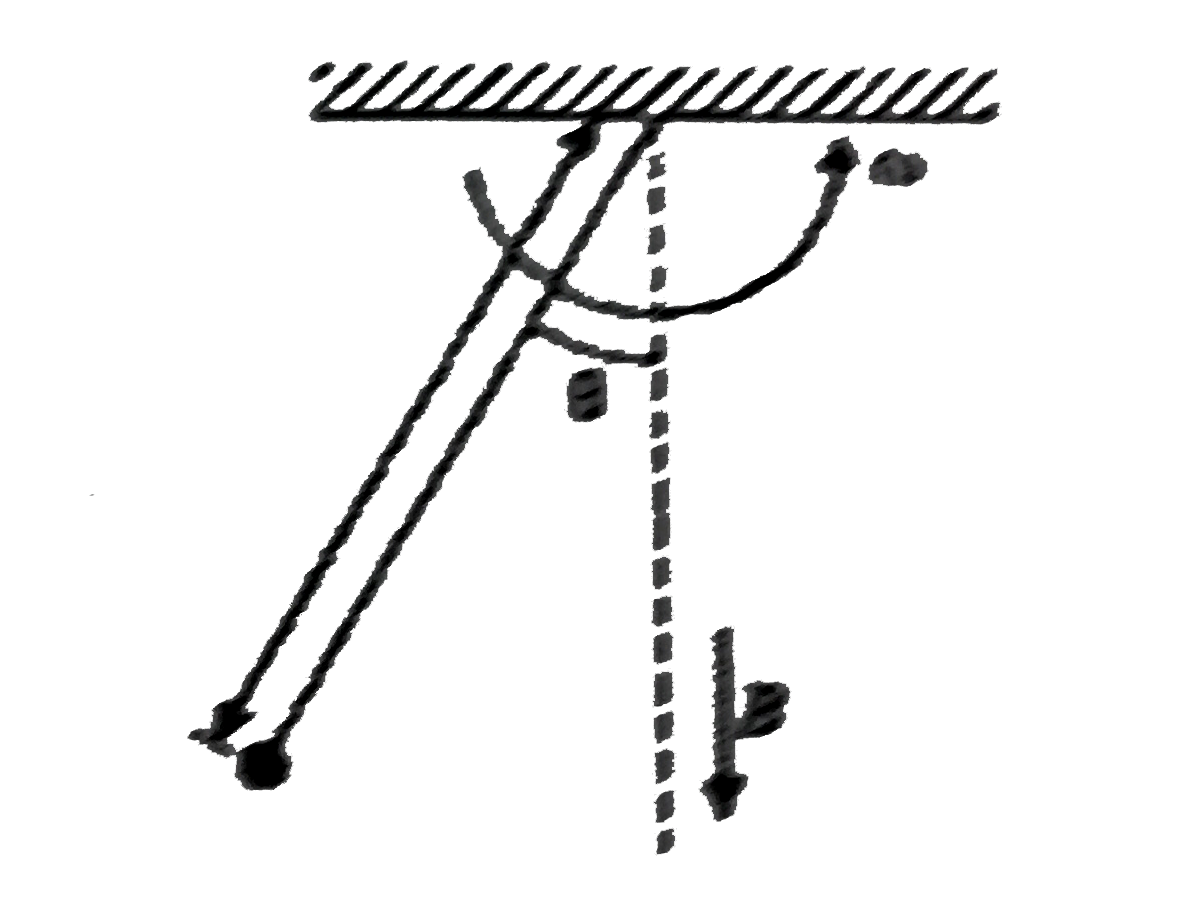
View SolutionA simple pendulum of length l ils pulled aside to make an angle θ with the vertical. Find the magnitude of the torque of the weitht w of the bob about the point of suspension. When is the torque zero?
View Solution
Knowledge Check
A simple pendulum of length l is set in motion such that the bob, of mass m, moves along a horizontal circualar path , and the string makes a constant angle θ with the vertical. The time period of rotation of the bob is l and the tension in the thread is T
At=2π√l/gBt=2π√lcosθ/gCT=4π2mlt2DThe bob is in equilibriumA heavy small sized sphere is suspended by a string of length l . The sphere rotates uniformly in a horizontal circle with the string making an angle θ with the vertical. Then the time period of this conical pendulum is-
AT = 2πBT=2π√(lsinθg)CT=2π√(lcosθg)DT=2π√(lg)A heavy small sized sphere is suspended by a string of length 2. The sphere is rotated uniformly in a horizontal circle with the string making an angle θwith the vertical. The time period of this conical pendulum is
A2π√ltanθgB2π√lcosθgC2π√1gD2π√lcosθg
Find the period of revolution of a conical simple pendulum whose thread of length l makes an angle α with the vertical (Fig).

View SolutionIf the string of a conical pendulum makes an angle θ with horizontal, then square of its time period is proportional to
View SolutionA simple pendulum is constructed by attaching a bob of mas m to a string of length L fixed at its upper end. The bob oscillates in a vertical circle. It is found that the speed of the bob is v when the string makes an angle θ with the vertical. Find the tension in the string at this instant.
View SolutionWhen the string of a conical pendulum makes an angle of 45∘ with the vertical , its time is T1 when the string makes an angle of 60∘ with the vertical , its time period is T2 then T21/T22is
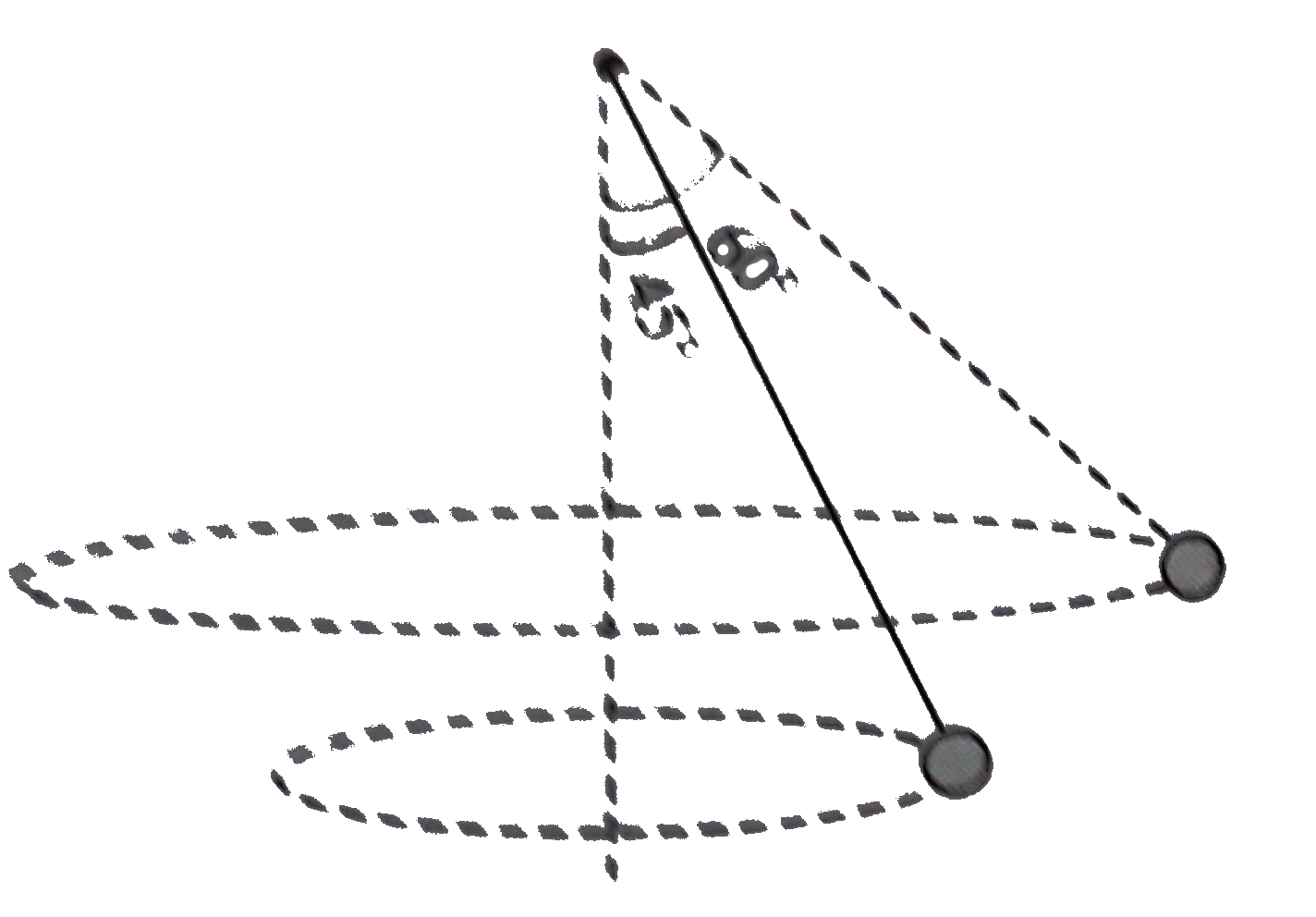
View SolutionA heavy & big sphere is hang with a string of length l. This sphere move in a horizontal circular path making an angle θ with vertical then its time period is
View Solution

