A mass is attached to the end of a string of length l which is tied to a fixed point O. The mass is released from the initial horizontal position of the string. Below the point O at what minimum distance a peg P should be fixed so that the mass turns about P and can describe a complete circle in the vertical plane?
(35)l
(25)l
l3
2l3
The correct Answer is:A
To solve the problem of determining the minimum distance a peg P should be fixed below point O so that a mass attached to a string can describe a complete circle in a vertical plane, we can follow these steps:
1. Understanding the Setup:
- A mass m is attached to a string of length L and is released from a horizontal position.
- The mass will swing down due to gravity and will gain kinetic energy as it descends.
2. Energy Conservation:
- At the highest point (initial position), the potential energy is maximum and kinetic energy is zero.
- At the lowest point (just before it swings around peg P), the potential energy is minimum and kinetic energy is maximum.
- Using conservation of energy, we can set up the equation:
mgh=12mv2
- Here, h is the vertical drop, which is equal to L (the length of the string).
3. Calculating Velocity at the Lowest Point:
- The potential energy at the highest point is mgL.
- The kinetic energy at the lowest point is:
12mv2=mgL
- Canceling m from both sides gives:
12v2=gL⟹v2=2gL⟹v=√2gL
4. Condition for Completing the Circle:
- For the mass to complete a vertical circle around peg P, it must have sufficient speed at the top of the circle.
- The minimum speed vt at the top of the circle (radius R) is given by:
vt=√gR
- At the lowest point, the radius R is the distance from peg P to the mass, which is L−x where x is the distance OP.
5. Setting Up the Equation:
- At the lowest point, the speed must satisfy:
√2gL=√gR
- Substituting R=L−x:
√2gL=√g(L−x)
6. Squaring Both Sides:
- Squaring both sides gives:
2gL=g(L−x)
- Canceling g from both sides:
2L=L−x
7. Solving for x:
- Rearranging gives:
x=L−2L=−L
- This means:
x=L−2L=−L⟹x=L/3
8. Finding the Distance OP:
- Since OP=x, we have:
OP=2L5
Conclusion:
The minimum distance OP below point O should be 2L5 for the mass to complete the circular motion.
- A mass m is attached to a string of length L and is released from a horizontal position.
- The mass will swing down due to gravity and will gain kinetic energy as it descends.
- At the highest point (initial position), the potential energy is maximum and kinetic energy is zero.
- At the lowest point (just before it swings around peg P), the potential energy is minimum and kinetic energy is maximum.
- Using conservation of energy, we can set up the equation:
mgh=12mv2
- Here, h is the vertical drop, which is equal to L (the length of the string).
- The potential energy at the highest point is mgL.
- The kinetic energy at the lowest point is:
12mv2=mgL
- Canceling m from both sides gives:
12v2=gL⟹v2=2gL⟹v=√2gL
- For the mass to complete a vertical circle around peg P, it must have sufficient speed at the top of the circle.
- The minimum speed vt at the top of the circle (radius R) is given by:
vt=√gR
- At the lowest point, the radius R is the distance from peg P to the mass, which is L−x where x is the distance OP.
- At the lowest point, the speed must satisfy:
√2gL=√gR
- Substituting R=L−x:
√2gL=√g(L−x)
- Squaring both sides gives:
2gL=g(L−x)
- Canceling g from both sides:
2L=L−x
- Rearranging gives:
x=L−2L=−L
- This means:
x=L−2L=−L⟹x=L/3
- Since OP=x, we have:
OP=2L5
The minimum distance OP below point O should be 2L5 for the mass to complete the circular motion.
Topper's Solved these Questions
- CIRCULAR MOTIONBook:DC PANDEYChapter:CIRCULAR MOTIONExercise:Match the columns
Explore 3 Videos
- CIRCULAR MOTIONBook:DC PANDEYChapter:CIRCULAR MOTIONExercise:Medical entrances s gallery
Explore 19 Videos
- CIRCULAR MOTIONBook:DC PANDEYChapter:CIRCULAR MOTIONExercise:Check point
Explore 45 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEYChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 2 Subjective
Explore 21 Videos
- COMMUNICATION SYSTEMBook:DC PANDEYChapter:COMMUNICATION SYSTEMExercise:Only One Option is Correct
Explore 27 Videos
Similar Questions
A particle of mass 1kg is attached to a string of length 5m. The string is attached to a fixed point O. It is released from the position as shown in Fig. Calculate
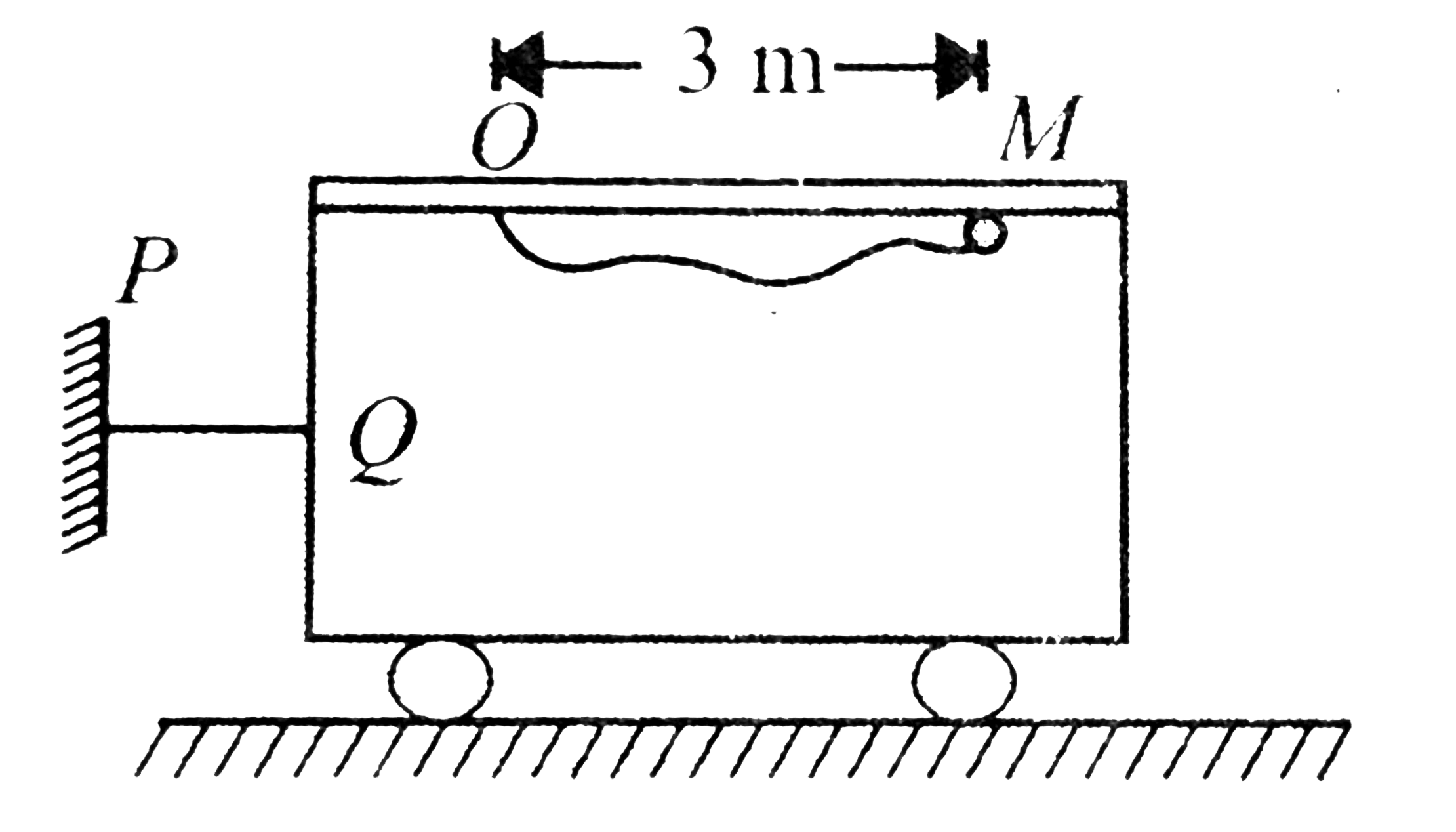
a. the impulse developed in the string when it becomes taut,
b. the velocity of the particle just after the string becomes taut,
c. the impulse developed in this string PQ at this instant.
View SolutionA small ball of mass 100g is attached to a light and inextensible string of length 50cm. The string is tied to a support O and the mass m released from point A which is a' a horizontal distance of 30cm from the support. Calculate the speed of the ball is its lowest point of the trajectory.
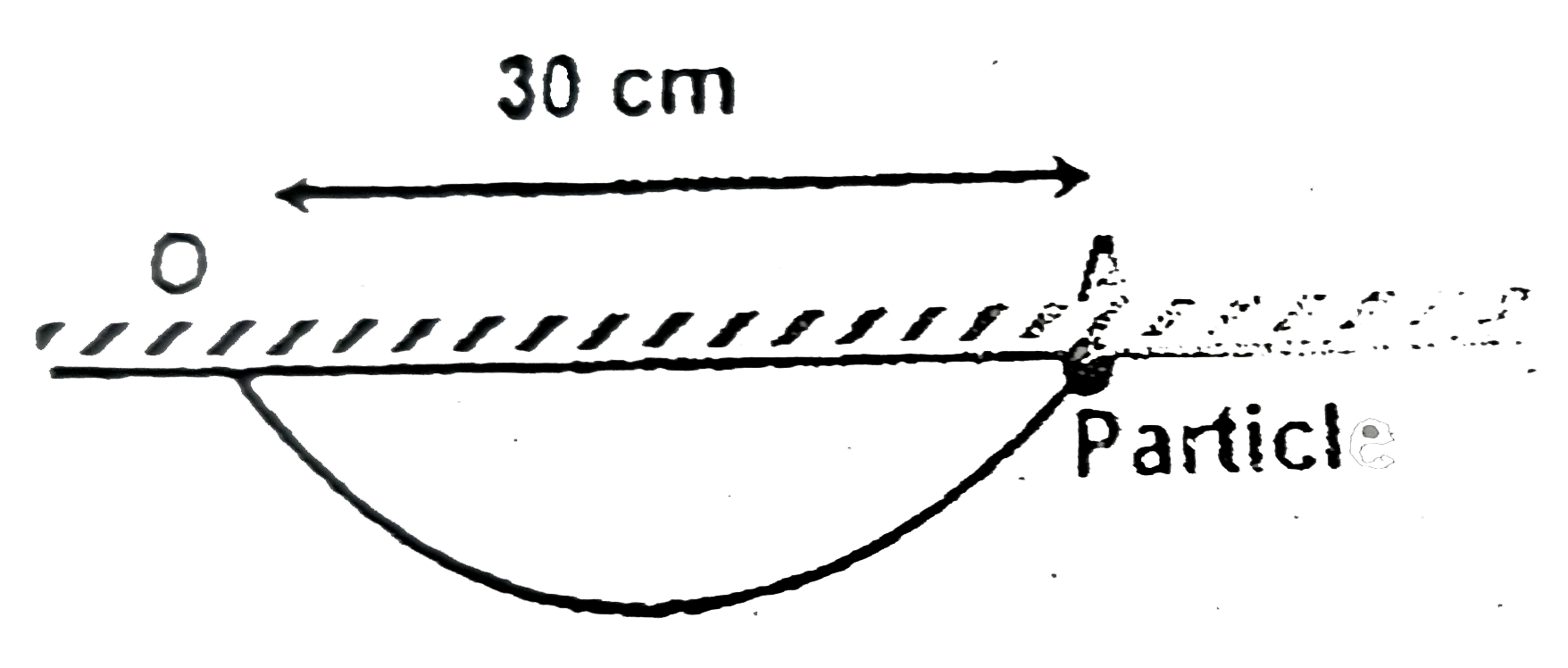
View Solution
Knowledge Check
A particle of mass m attached to the end of string of length l is released from the horizontal position. The particle rotates in a circle about O as shown When it is vertically below O, the string makes contact with a nail N placed directly below O at a distance h and rotates around it. For the particle to swing completely around the nail in a circle.
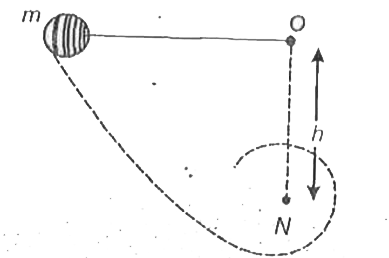 Ah<35lBh≥35lCh<25lDh≥25l
Ah<35lBh≥35lCh<25lDh≥25lA particle of mass m is suspended from a string of length l fixed to the point O. What velocity should be imparted to the particle in its lowermost position so that the string is just able to reach the horizontal diameter of the circle?
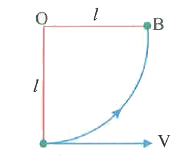 Av=√2glBv=√3glCv=√glDv=2gl
Av=√2glBv=√3glCv=√glDv=2glA bob of mass m attached with a string of length l tied to a point on ceiling is released from a position when its string is horizontal. At the bottom most point of its motion, an identical mass m gently stuck to it. Find the maximum angle from the vertical to which it rotates.
A(a) cos−1(23)B(b) cos−1(34)C(c) cos−1(14)D(d) 60∘
One end of a string of length 1.5 m is tied to a stone of mass 0.4 kg and the other end to a small pivot on a smooth vertical board. What is the minimum speed of the stone required at its lower most point so that the string does not slack at any point in its motion along the vertical circle ?
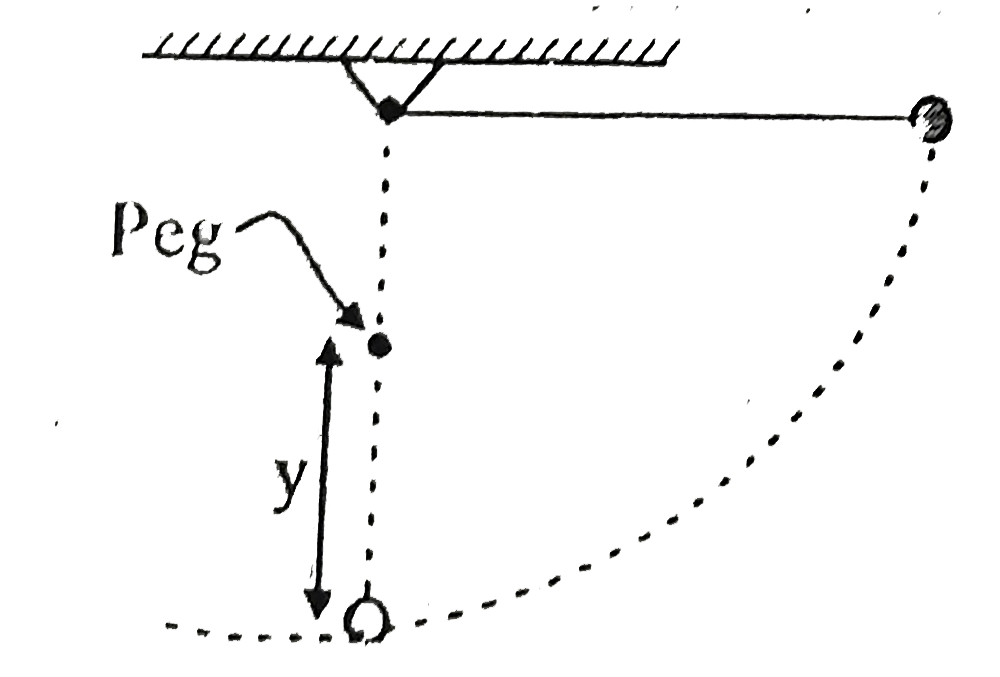
View SolutionA bob tied to an ideal string of length l is released from the horizontal position shown. A peg P whose height is adjustable, can arrest the free swing of the pendulum, as shown in Figure.
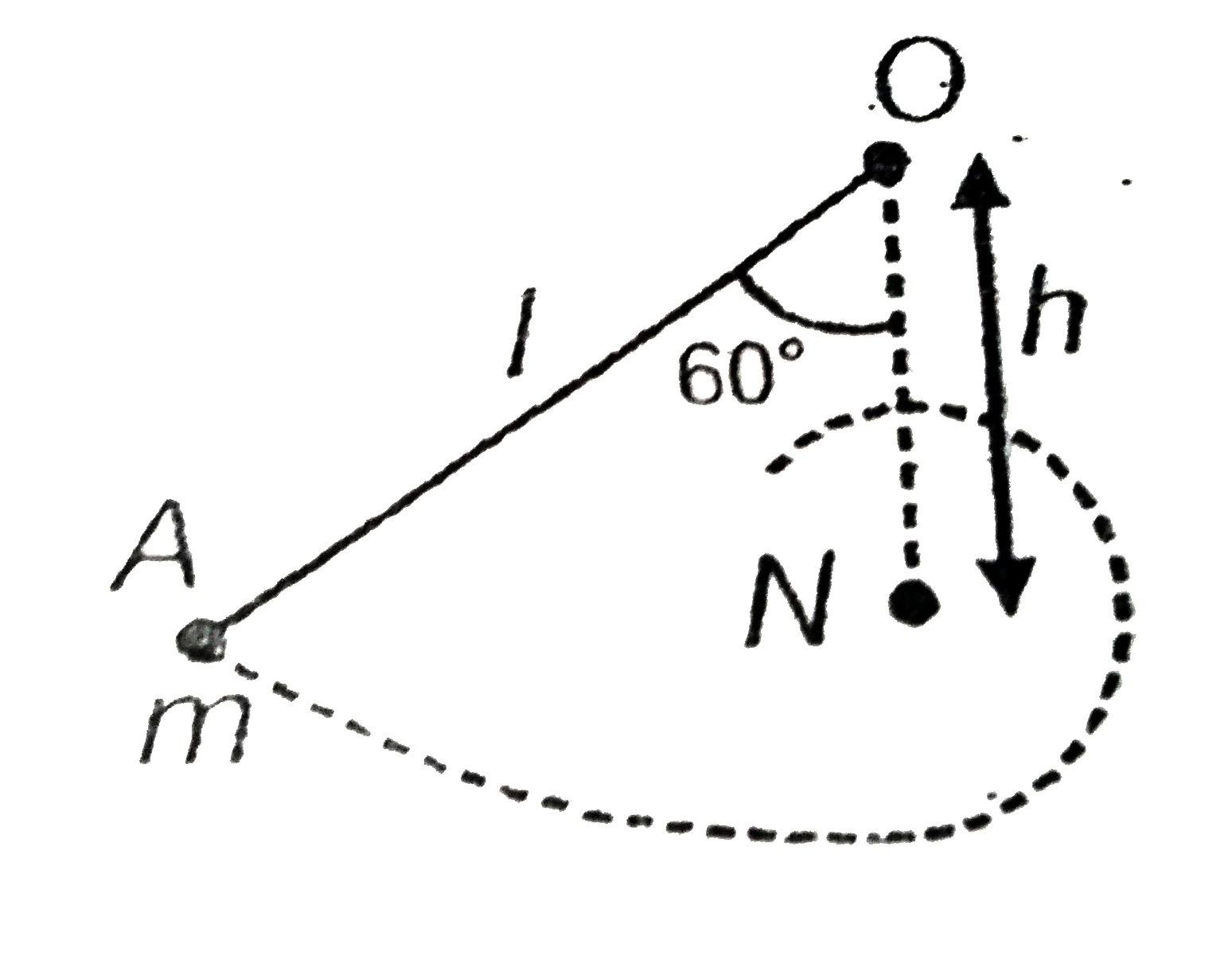
View SolutionA particle of mass m, attached to the end of string of length l is released from the initial position A as shown in the figures. The particle moves in a vertical circular path about O. When it is vetically below O, the string makes contact with nail N placed directly below O at distance h and rotat es around it. If the particle just complete the vertical circle about N,then
View SolutionA stone of mass 0.2 kg is tied to one end of a string of length 80cm Holding the other end, the stone is wirled into a vertical circle. What is the minimum speed of the stone at the lowest point so that it just completes the circle What is the tension in the string at the lowest point of the circular path ? . (g=10−2) .
View SolutionA particle of mass m is attached to one end of a string of length l while the other end is fixed to a point h above the horizontal table. The particle is made to revolve in a circle on the table so as to make p revolutions per second. The maximum value of p if the particle is to be in contact with the table will be :
View Solution

