Three masses, each equal to M are placed at the three corners of a square of side a. Calculate the force of attraction on unit mass at the fourth corner.
Gm3a2
Gm√3a2
3Gma2
Gma2(√2+12)
The correct Answer is:D
Step by step video solution for Three masses, each equal to M are placed at the three corners of a square of side a. Calculate the force of attraction on unit mass at the fourth corner. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
Three masses, each equal to M, are placed at the three corners of a square of side a. the force of attraction on unit mass at the fourth corner will be
View SolutionThree charges, each equal to q, are placed at the three. corners of a square of side a . Find the electric field at. the fourth corner.
View Solution
Knowledge Check
Six point masses of mass m each are at the vertices of a regular hexagon of side l. Calculate the force on any of the masses.
AGm2l2[54+1√3]BGm2l2[34+1√3]CGm2l2[54−1√3]DGm2l2[34−1√3]
Three charges, each equal to q, are placed at the three. corners of a square of side a . Find the electric field at. the fourth corner.
View SolutionFour point charges are placed at the corners of a square of side l. Calculate potential at the centre of square.
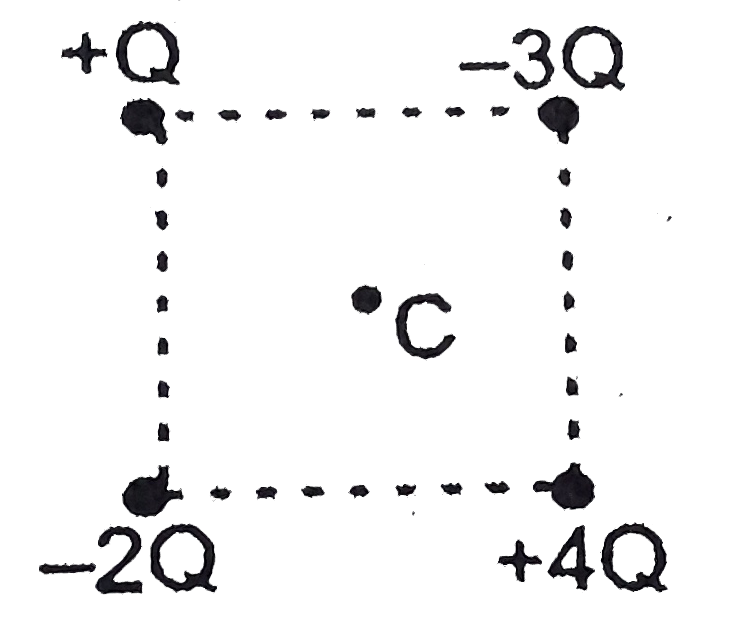
View SolutionThree equal masses each of mass 'm' are palced at the three corners of an equilateral of side a
If a fourth particle of equal mass is placed at the centre of triangle then net force acting on it is equal to .
View SolutionThree equal masses each of mass 'm' are palced at the three corners of an equilateral of side a
If a fourth particle of equal mass is placed at the centre of triangle then net force acting on it is equal to .
View SolutionFour equal masses (each of mass M) are placed at the corners of a square of side a. The escape velocity of a body from the centre O of the square is
View SolutionIf four different masses m1,m2,m3 and m4 are placed at the four corners of a square of side a, the resultant gravitational force on a mass m kept at the centre is
View SolutionSix point masses of mass m each are at the vertices of a regular hexagon of side l. Calculate the force on any of the masses.
View Solution
