In a diatiomic molecule, the rotational energy at a given temperature
does not obeys Maxwell.s distribution
have the same value for all molecules
equals the translations kinetic energy for each molecule
is (2/3)rd the translational kinetic energy for each molecule.
The correct Answer is:D
Step by step video solution for In a diatiomic molecule, the rotational energy at a given temperature by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
According to the law of equipartition of energy, internal energy of an ideal gas at a given temperature, is equally distributed in translational and rotational kinetic energies.
Rotational kinetic energy of a monoatomic gas is zero.
View SolutionWhich of the following paramenters is the same for molecules of all gases at a given temperature?
View SolutionIn the figure, the distribution of energy density of the radiation emitted by a black body at a given temperature is shown. The possible temperature of the black body is
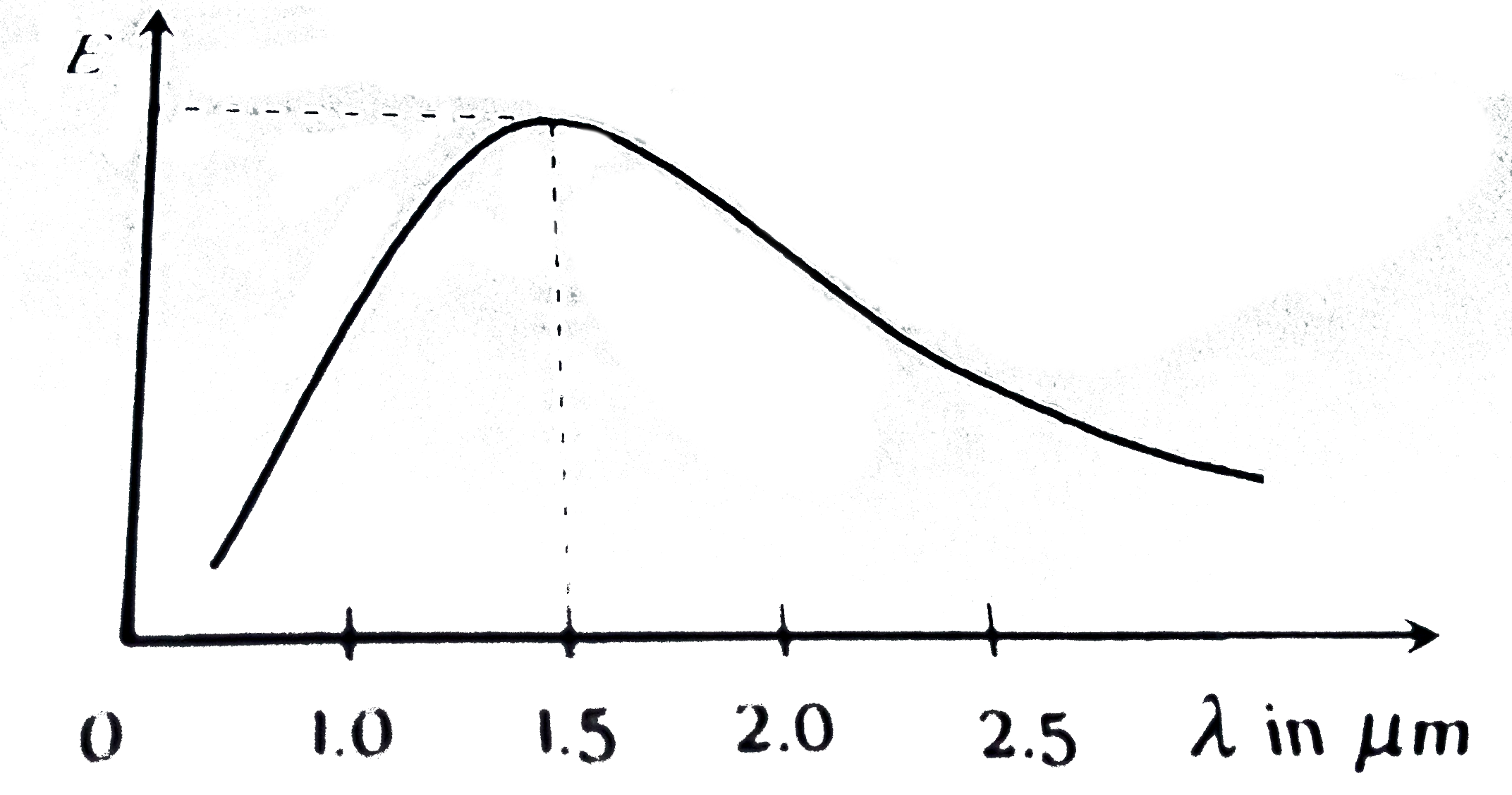
View SolutionAssertion Total internal energy of oxygen gas at a given temperature is E of this energy 35 E is rotational kinetic energy.
Reason Potantial energy of an ideal gas is zero.
View SolutionThe translational kinetic energy of one mole oxygen gas at a temperature is 15x10−20J. Its rotational kinetic energy at same temperature is
View SolutionThe ratio of translational and rotational kinetic energies at 100K temperature is 3:2. Then the internal energy of one mole gas at that temperature is (R=8.3j/mol−K]
View SolutionStatement-1. Most probable velocity is the velocity possesed by the maximum fraction of the molecules at a given temperature.
Statement-2. On collision, more and more molecules acquire higher speed at the same temperature.
View SolutionAt ordinary temperatures, the molecules of an ideal gas have only translational and rotational kinetic energies. At high temperatures they may also have vibrational energy.
As a result of this, at higher temperature
View SolutionAt ordinary temperatures, the molecules of an ideal gas have only translational and rotational kinetic energies. At high temperatures they may also have vibrational energy.
As a result of this, at higher temperature
View SolutionAt ordinary temperatures, the molecules of an ideal gas have only translational and rotational kinetic energies. At high temperatures, they may also have vibrational energy. As a result of this, at higher temperatures, molar specific heat capacity at constant volume, CV is
View Solution
