P is a point at a distance r from the centre of a spherical shell of mass M and radius a, where r<a The gravitational potential at P is
−GMr
−GMa
−GMra2
−GM(a−ra2)
The correct Answer is:B
To find the gravitational potential at point P, which is located at a distance r from the center of a spherical shell of mass M and radius a, where r<a, we can follow these steps:
Step 1: Understand the Concept of Gravitational Potential
Gravitational potential U at a point in space due to a mass M is given by the formula:
U=−GMr
where G is the gravitational constant, M is the mass creating the gravitational field, and r is the distance from the mass to the point where the potential is being calculated.
Step 2: Apply the Shell Theorem
According to the shell theorem, the gravitational potential inside a uniform spherical shell of mass is constant and equal to the potential at the surface of the shell. Therefore, for any point inside the shell (where r<a), the gravitational potential U is given by:
U=−GMa
where a is the radius of the shell.
Step 3: Write the Final Expression for Gravitational Potential at Point P
Since point P is inside the shell, we can directly use the expression derived from the shell theorem:
U=−GMa
Conclusion
Thus, the gravitational potential at point P, located at a distance r from the center of the spherical shell, is:
U=−GMa
Gravitational potential U at a point in space due to a mass M is given by the formula:
U=−GMr
where G is the gravitational constant, M is the mass creating the gravitational field, and r is the distance from the mass to the point where the potential is being calculated.
According to the shell theorem, the gravitational potential inside a uniform spherical shell of mass is constant and equal to the potential at the surface of the shell. Therefore, for any point inside the shell (where r<a), the gravitational potential U is given by:
U=−GMa
where a is the radius of the shell.
Since point P is inside the shell, we can directly use the expression derived from the shell theorem:
U=−GMa
Thus, the gravitational potential at point P, located at a distance r from the center of the spherical shell, is:
U=−GMa
Similar Questions
A particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the centre.
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the centre.
View Solution
Knowledge Check
A particle of mass M is placed at the centre of a spherical shell of same mass and radius a. What will be the magnitude of the gravitational potential at a point situated at a/2 distance from the centre ?
A−3GMRB−2GMRC−GMRD−4GMRA particle of mass m is placed at the centre of a unifrom spherical shell of mass 3 m and radius R The gravitational potential on the surface of the shell is .
AGMRB−GMRC−4GMRD−2GMR
A particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the center.
View SolutionA block of mass m is lying at a distance r from a spherical shell of mass m and radius r, then :
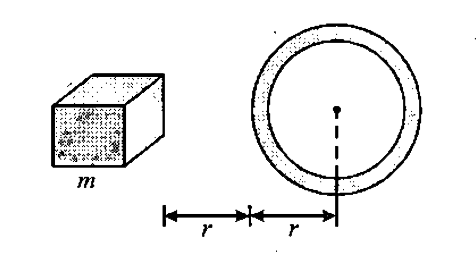
A. only gravitational field inside the shell is zero
B. gravitational field and gravitational potential both are zero inside the shell
C. gravitational potential as well as gravitational field inside the shell are not zero .
D. can't be ascertained
View SolutionA point charge q is placed at a distance of r from the centre O of an uncharged spherical shell of inner radius R and outer radius 2R. The electric potential at the centre of the shell will be

View SolutionA hollow spherical shell is compressed to half its radius. The gravitational potential at the centre
View SolutionA charge q is placed at a distance of 2R from the centre of a spherical conducting shell of radius R. What is electrical potential, due to charges induced on the shell, at a point which is farthest from the point charge ?
View SolutionA body of mass m is placed at the centre of the spherical shell of radius R and mass M. The gravitation potential on the surface of the shell is
View Solution
