State the relation between the escape and orbital velocities. Does this relation change with height ?
To solve the problem, we need to establish the relationship between escape velocity and orbital velocity, and determine if this relationship changes with height.
1. Define Escape Velocity:
The escape velocity (ve) is the minimum velocity required for an object to break free from the gravitational attraction of a planet without any further propulsion. The formula for escape velocity is given by:
ve=√2gR
where g is the acceleration due to gravity at the surface of the planet and R is the radius of the planet.
2. Define Orbital Velocity:
The orbital velocity (vo) is the velocity required for an object to maintain a stable orbit around a planet. The formula for orbital velocity is given by:
vo=√gR
3. Establish the Relationship:
To find the relationship between escape velocity and orbital velocity, we can take the ratio of escape velocity to orbital velocity:
vevo=√2gR√gR
Simplifying this gives:
vevo=√2
Therefore, we can express the relationship as:
ve=√2⋅vo
4. Check if the Relation Changes with Height:
The formulas for escape velocity and orbital velocity depend on the radius of the planet and the acceleration due to gravity. When we consider height, the acceleration due to gravity (g) changes with height, but the ratio of escape velocity to orbital velocity remains:
vevo=√2
This indicates that the relationship does not change with height, as the R terms cancel out when taking the ratio.
Final Answer:
The relationship between escape velocity and orbital velocity is given by:
ve=√2⋅vo
This relationship does not change with height.
The escape velocity (ve) is the minimum velocity required for an object to break free from the gravitational attraction of a planet without any further propulsion. The formula for escape velocity is given by:
ve=√2gR
where g is the acceleration due to gravity at the surface of the planet and R is the radius of the planet.
The orbital velocity (vo) is the velocity required for an object to maintain a stable orbit around a planet. The formula for orbital velocity is given by:
vo=√gR
To find the relationship between escape velocity and orbital velocity, we can take the ratio of escape velocity to orbital velocity:
vevo=√2gR√gR
Simplifying this gives:
vevo=√2
Therefore, we can express the relationship as:
ve=√2⋅vo
The formulas for escape velocity and orbital velocity depend on the radius of the planet and the acceleration due to gravity. When we consider height, the acceleration due to gravity (g) changes with height, but the ratio of escape velocity to orbital velocity remains:
vevo=√2
This indicates that the relationship does not change with height, as the R terms cancel out when taking the ratio.
The relationship between escape velocity and orbital velocity is given by:
ve=√2⋅vo
This relationship does not change with height.
Similar Questions
Knowledge Check
The relation between Y. η and B is
A1Y=13η+19BB9Y=1η+3BC1η=1B+1YD9Y=3η+1B
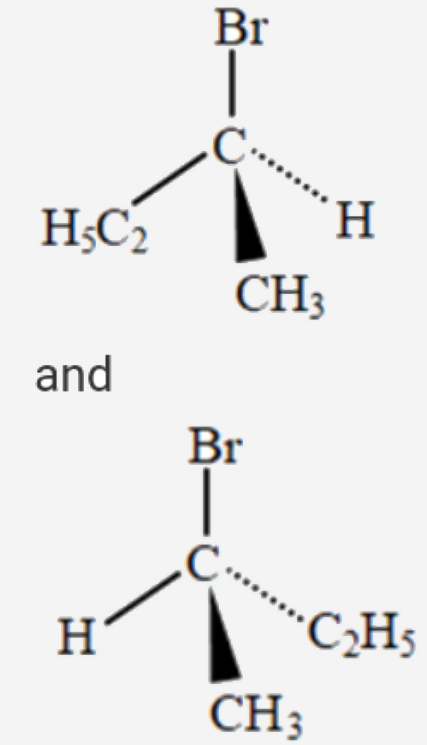
The relation between given pair is
View SolutionWhat is the relation between Speed and distance.
View SolutionState the relation between atm, Nm, Pa, torr and bar.
View Solution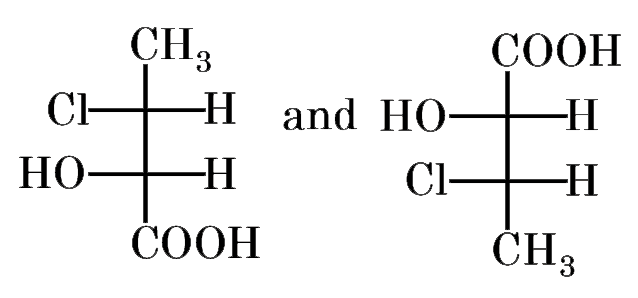
relation between given pairs is:
View SolutionThe relation between the particles velocity and wave velocity is -
View SolutionThe relation between given compound is :-

View SolutionGive Relation between Force and work.
View Solution

_S01_028_Q01.png)