Variation of acceleration due to gravity (g) with distance x from the centre of the Earth is best represented by ( R → Radius of the Earth )
Step by step video solution for Variation of acceleration due to gravity (g) with distance x from the centre of the Earth is best represented by ( R rarr Radius of the Earth ) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
The dependence of acceleration due to gravity g on the distance r from the centre of the earth, assumed to be a sphere of radius R of uniform density is as shown in Fig. below:

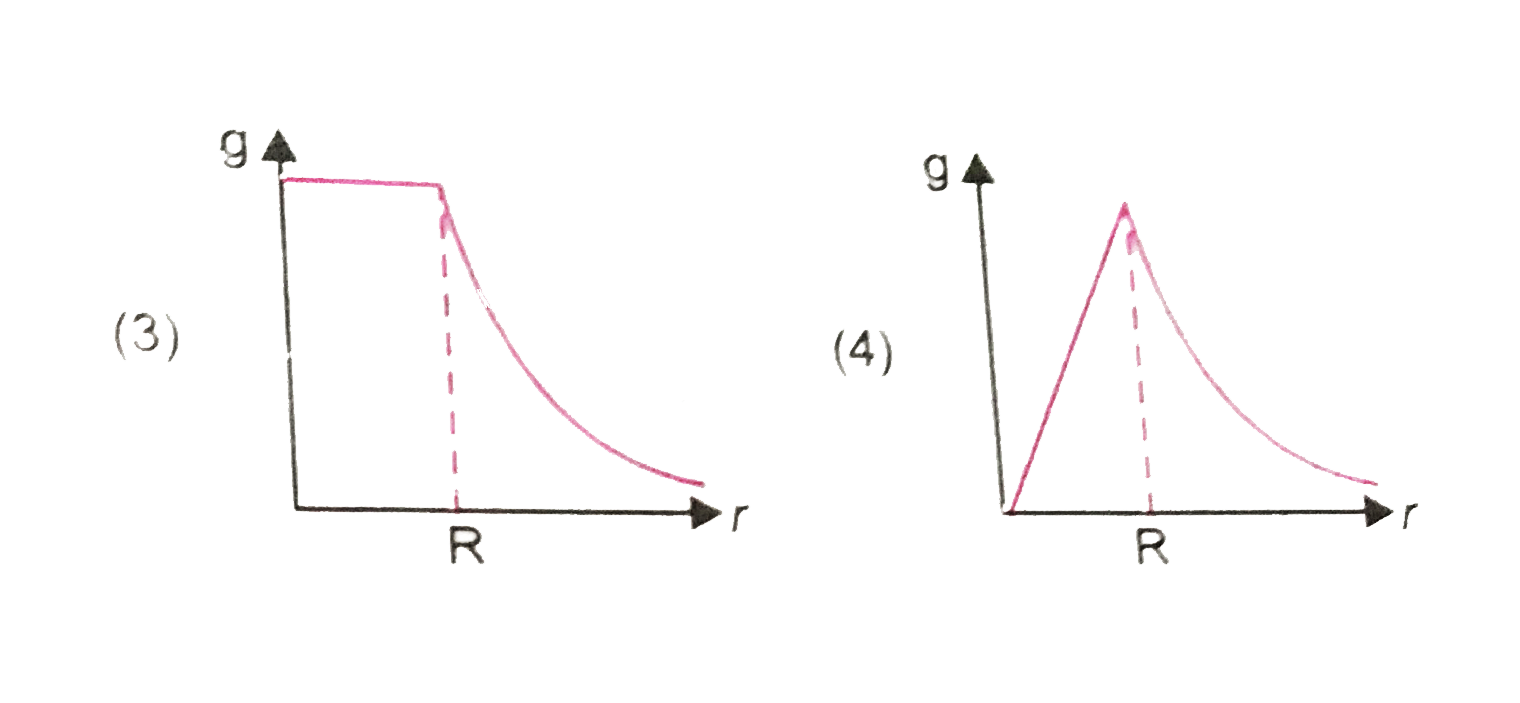
The correct figure isA(i)B(ii)C(iii)D(iv)Acceleration due to gravity at any point inside the earth
Avaries inversely as the square of the distance from the centreBis independent of the distance from the centreCis directly proportional to the distance from the centreDis inversely proportional to the distance from centre
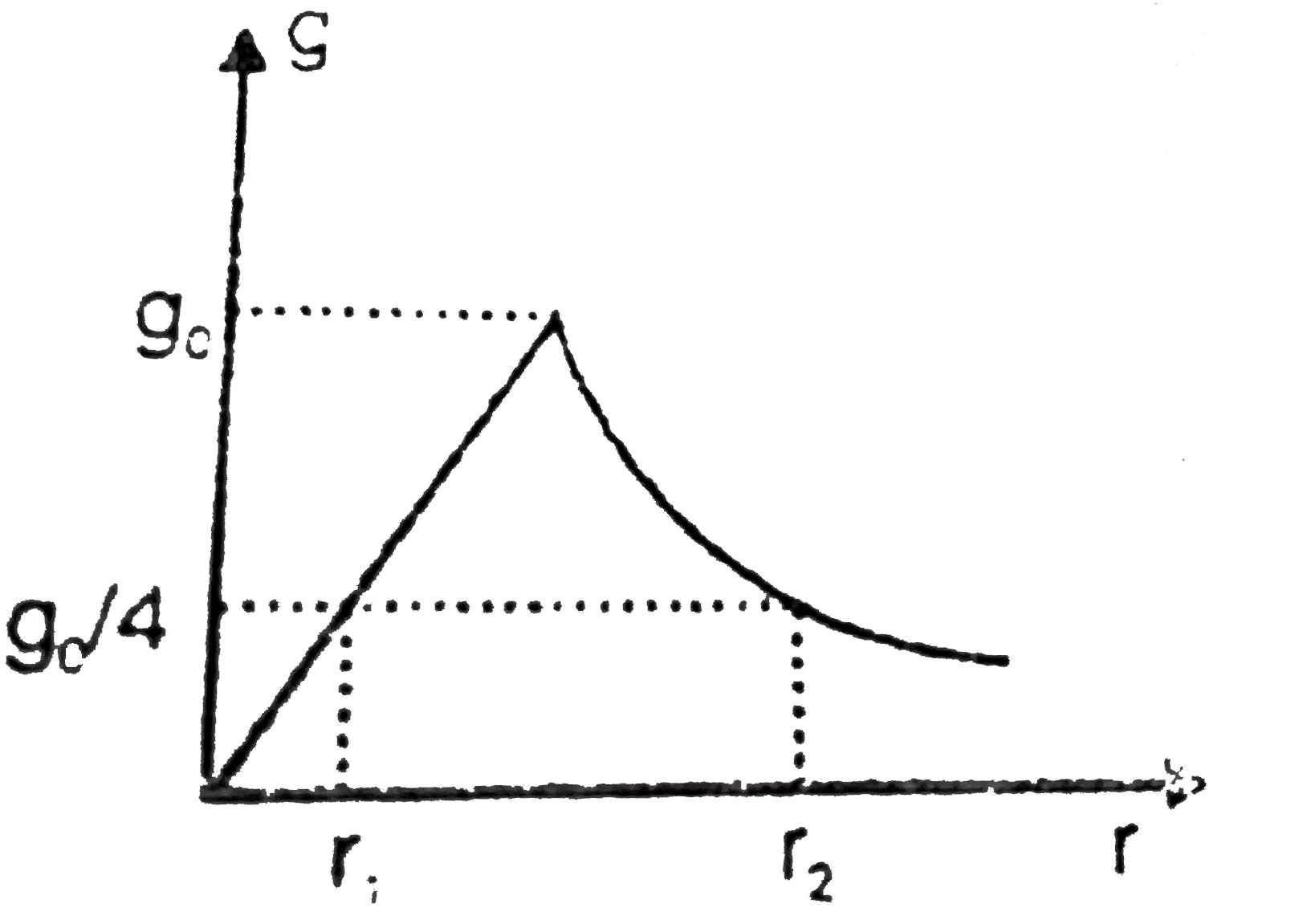
Figure shows variation of acceleration due to gravity with distance from centre of a uniform spherical planet, Radius of planet is R. What is r1−r1
View SolutionA satellite of mass m is moving in a circular or orbit of radius R around the earth. The radius of the earth is r and the acceleration due to gravity at the surface of the earth is g. Obtain expressions for the following :
(a) The acceleration due to gravity at a distance R from the centre of the earth
(b) The linear speed of the satellite
(c ) The time period of the satellite
View SolutionIf acceleration due to gravity at distance d [<R] from the centre of earth is β , then its value at distance d above the surface of earth will be [ where R is radius of earth ]
View SolutionWhich graph correctley presents the variation of acceleration due to gravity with the distance form the centre of the earth?
View SolutionHow is the acceleration due to gravity on the surface of the earth related to its mass and radius ?
View SolutionIf g is the acceleration due to gravity on the surface of the earth , its value at a height equal to double the radius of the earth is
View Solution
