The largest and the shortest distance of the earth from the sun are r1 and r2. Its distance from the sun when it is perpendicular to the major axis of the orbit drawn from the sun
Since e=ca⇒c=ea ∴r1=a+c=a+ea=a(1+e)
r2=a−c=a−ea=a(1−e)
Required distance L=b2a (semi latus rectum )
we have r1+r2=2a and r−r_2=a(1+e)−a(1−e)=2ae⇒e=r1−r2r1+r2
Also b2=a2(1−e2)
∴L=b2a=a2(1−e2)a=a(1−e2)
=(r1+r22)[1−(r1−r2r1+r2)2]
on simplification , L=2r1r2r1+r2or 2L=1r1+1r2
Similar Questions
Knowledge Check
Average distance of the earth from the sun is L1. If one year of the earth =D days, one year of another planet whose average distance from the sun is L2 will be
AD(L2L1)1/2 daysBD(L2L1)3/2 daysCD(L2L1)2/3 daysDD(L2L1) daysA planet is revolving in an elliptical orbit around the sun. Its closest distance from the sun is r and the farthest distance is R. If the velocity of the planet nearest to the sun be v and that farthest away from the sun be V. then v/V is
AR2/r2Br2/R2CR/rDr/R
A planet of mass m moves around the Sun of mass Min an elliptical orbit. The maximum and minimum distance of the planet from the Sun are r1 and r2, respectively. Find the relation between the time period of the planet in terms of r1 and r2.
View SolutionAssuming the average distance of the earth from the sun to be 149700000 km and the angle subtended by the sun at the eye of a person on the earth to be 32', find the sun's diameter.
View SolutionA planet is revolving around the Sun in an elliptical orbit. Its closest distance from the sun is rmin. The farthest distance from the sun is rmax if the orbital angular velocity of the planet when it is nearest to the Sun ω then the orbital angular velocity at the point when it is at the farthest distance from the sun is
View SolutionThe ratio of mean distances of three planets from the sun are 0.5:1:1:5, then the square of time periods are in the ratio of
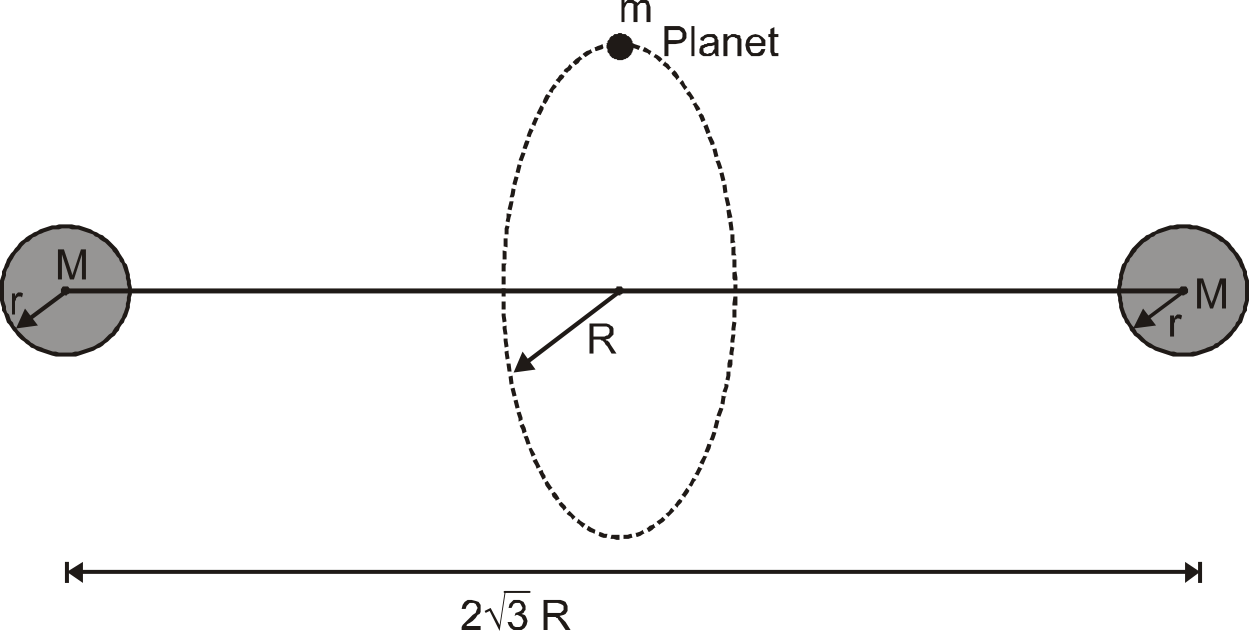
View SolutionConsider a hypothetical solar system, which has two identical massive suns each of mass M and radius r, seperated by a seperation of 2√3R (centre to centre). (R gtgtgtr). These suns are always at rest. There is only one planet in this solar system having mass m. This planet is revolving in circular orbit of radius R such that centre of the orbit lies at the mid point of the line joining the centres of the sun and plane of the orbit is perpendicular to the line joining the centres of the sun. Whole situation is shown in the figure.
View SolutionCompare the distance of the sun from the earth and the distance of the mars from the Earth if the Sun is 1.5×108 km from the Earth and the Mars is 5.5×107 km from the Earth.
View Solution