Let the speed of the planet at the perhelion Pin Fig. 8.1 (a) be vp and the sun-planat distance SP be rp. Relate (rp'vp) to the corresponding quantities at the aphelion (rA.vA) will the planat take equal times to traverse BAC and CPB?
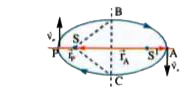
According to law of conservation of angular momentum. Angular momentum of the planet at P= Angular momentum of the planet at A
⇒=mVprp=mVArAor VPVA=rArP
Since rA>rP so VP>VA
Here area SBAC is greater than the area SCPB. According to Kepler.s second law, as the areal velocity of the planet is constant around the sun, i.e equal areas are swept on equal times, the planet will take longer time to traverse BAC than CPB.
Similar Questions
Let the speed of the planet at the perihelion P in figure be vP and the Sun planet distance SP be rP. Relater rP,vP to the corresponding quantities at the aphelion (rA,vA). Will the planet take equal times to transverse BAC and CPB?

View SolutionLet V and I respresent, respectively, the readings of the voltmeter and ammetre shows in Fig. 6.34, and let RV and RV be their equivalent resistances. Because of the resistances of the meters, the resistnce R is not simply equal to V/I.
(a) When the circuit is connected as shows in Fig. 6.34 (a), shows that R=VI−RA
Explain why the true resistance R is always less than V/I.
(b) When the connections are as shows in Fig.6.34 (b)
Show that R=VI−(V/RV)
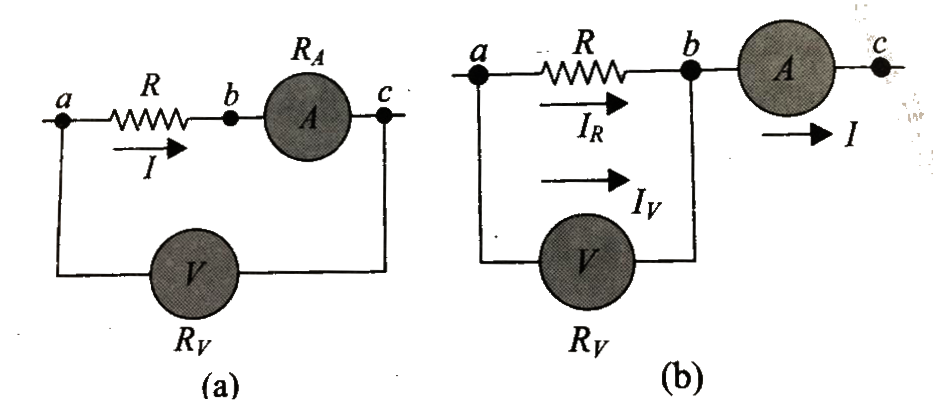
Explain why the true resistance R is always greater than V/I.
(c ) Show that the power delivered to the resistor in part
(i) is IV−I2RA and that in part (ii) is IV−(V2/RV)
View Solution
Knowledge Check
A planet orbits the sun in an elliptical path as shown in the figure. Let vp and vA be spped of the planet when at perohelion and aphelion respectively. Which of the following relations is correct ?
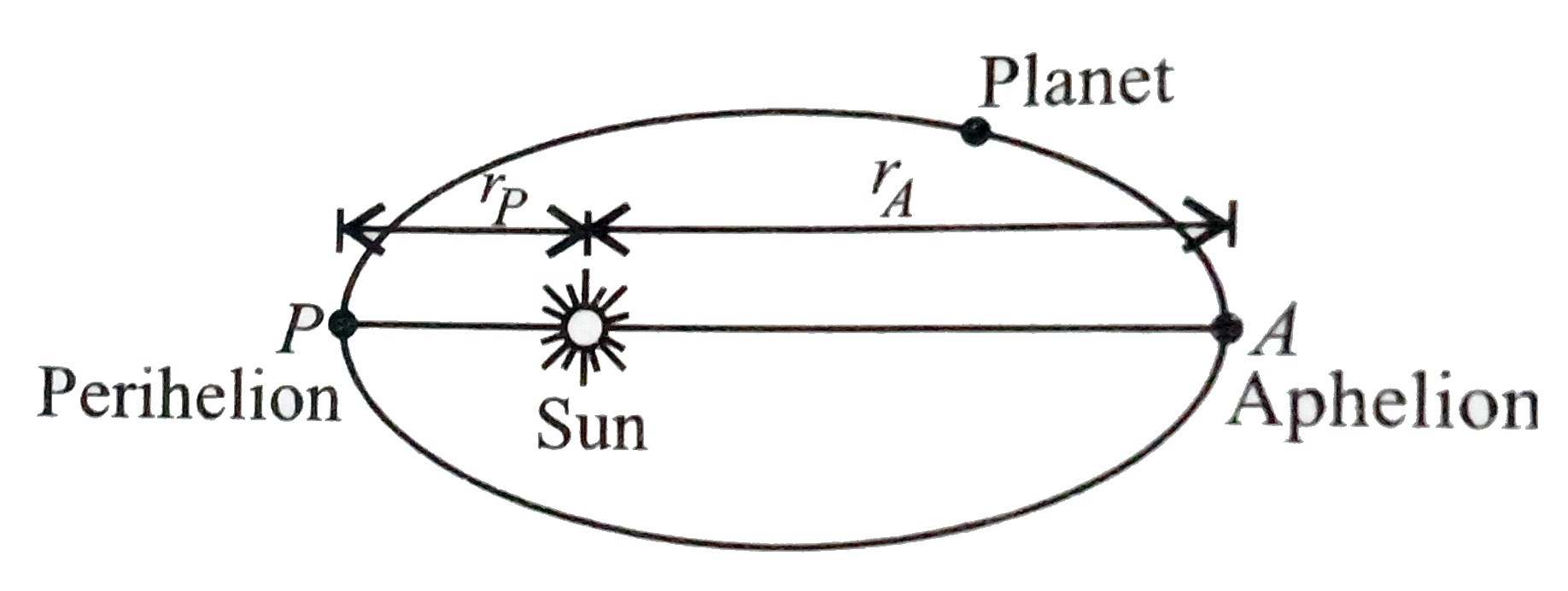 ArprA=vAvpBrprA=vpvACrprA=√vpvADrprA=√vAvp
ArprA=vAvpBrprA=vpvACrprA=√vpvADrprA=√vAvpA planet is revolving in an elliptical orbit around the sun. Its closest distance from the sun is r and the farthest distance is R. If the velocity of the planet nearest to the sun be v and that farthest away from the sun be V. then v/V is
AR2/r2Br2/R2CR/rDr/R
A satellite of mass m orbits the earth in an elliptical orbit having aphelion distance ra and perihelion distance rp. The period of the orbit is T. The semi-major and semi-minor axes of the ellipse are ra+rp2 and √rpra respectively. The angular momentum of the satellite is: (A) 2mπ(rB+rp)√rarpT (B) mπ(ra+rp)√rarp2T (C) mπ(ra+rp)√rarp4T (D) mπ(ra+rp)√rarpT
View SolutionA plenet moving along an elliptical orbit is closest to the sun at a distance r1 and farthest away at a distance of r2. If v1 and v2 are the linear velocities at these points respectively, then the ratio v1v2 is
View SolutionA planet of mass m revolves in elliptical orbit around the sun of mass M so that its maximum and minimum distance from the sun equal to ra and rp respectively. Find the angular momentum of this planet relative to the sun.
View SolutionThe pressure p and the volume v of a gas are connected by the relation pv1.4=const. Find the percentage error in p corresponding to a decrease of % in v.
View SolutionA planet is revolving around the sun. its distance from the sun at apogee is rA and that at perigee is rp. The masses of planet and sun are 'm' and M respectively, VA is the velocity of planet at apogee and VP is at perigee respectively and T is the time period of revolution of planet around the sun, then identify the wrong answer.
View SolutionA planet is revolving round the sun is elliptical orbit. Velocity at perigee position ( nearest) is v1 and at apogee position ( farthest) is v2. Both these velocities are perpendicular to the line joining centre of sun and planet. r1 is the minimum distance and r2 the maximum distance.
At apogee position suppose speed of planet is slightly decreased from v2, then what will happen to minimum distance r1 and maximum distance r2 in the subsequent motion.
View Solution
