The mass density of a spherical body is given by ρ(r)=kr for r≤R and ρ(r)=0for r > R , where r is the distance from the centre. The correct graph that describes qualitatively the acceleration, a, of a test particle as a function of r is :
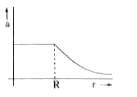
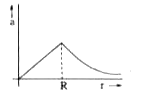
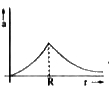
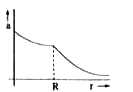
The correct Answer is:A
Step by step video solution for The mass density of a spherical body is given by rho(r)=k/r for r le R and rho (r)=0for r > R , where r is the distance from the centre. The correct graph that describes qualitatively the acceleration, a, of a test particle as a function of r is : by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
Find the gravitational potential due to a spherical shell of mass M and radius R at r<R and r>R, where r is the distance from the centre of the shell.
View SolutionLet there be a spherical symmetric charge density varying as p(r)=p0rR upto r = R and ρ(r)=0 for r>R, where r is the distance from the origin. The electric field at on a distance r(r<R) from the origin is given by -
View SolutionThe density inside a solid sphere of radius a is given by ρ=ρ0r, where ρ0 is the density at the surface and r denotes the distance from the centre. Find the gravitational field due to this sphere at a distance 2a from its centre.
View SolutionThe potential energy function of a particle is given by U(r)=A2r2−B3r, where A and B are constant and r is the radial distance from the centre of the force. Choose the correct option (s)
View SolutionLet there be a spherically symmetric charge distribution with charge density varying as ρ(r)=ρ(54−rR) upto r=R, and ρ(r)=0 for r>R, where r is the distance from the origin. The electric field at a distance r(rltR) from the origin is given by
View SolutionThe density inside a solid sphere of radius a is given by ρ=ρ0r, where ρ0 is the density ast the surface and r denotes the distance from the centre. Find the graittional field due to this sphere at a distance 2a from its centre.
View SolutionThe mass density of a spherical galaxy varies as Kr over a large distance 'r' from its centre . In that region , a small star is in a circular orbit of radius R . Then the period of revolution , T depends on R as :
View SolutionCharge density of a sphere of radius R is ρ=ρ0r where r is distance from centre of sphere.Total charge of sphere will be

View SolutionLet a total charge 2Q be distributed in a sphere of radius R, with the charge density given by , ρ(r)=kr, where r is the distance from the centre. Two charge A and B, of –Q each, are placed on diametrically opposite points, at equal distance, a from the centre. If A and B do not experience any force, then:
View SolutionThe potential energy of a particle in a force field is:
U=Ar2−Br,. Where A and B are positive
constants and r is the distance of particle from the centre of the field. For stable equilibrium the distance of the particle is
View Solution
