The mass density of a spherical body is given by ρ(r)=kr for r≤R and ρ(r)=0for r > R , where r is the distance from the centre. The correct graph that describes qualitatively the acceleration, a, of a test particle as a function of r is :
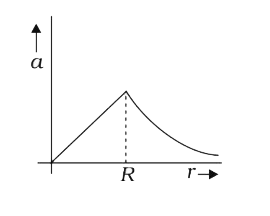
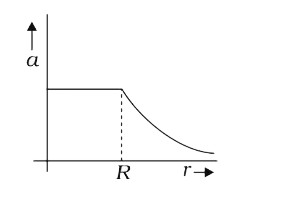
The correct Answer is:B
To solve the problem, we need to analyze the mass density of the spherical body and how it affects the acceleration of a test particle at different distances from the center of the sphere.
1. Understanding the Mass Density:
The mass density is given by:
ρ(r)=krfor r≤R
ρ(r)=0for r>R
This indicates that the mass density decreases as we move away from the center of the sphere until we reach the radius R.
2. Finding the Mass Inside Radius r:
To find the total mass M within a radius r (where r≤R), we need to integrate the density over the volume:
M=∫r0ρ(r)dV
The volume element in spherical coordinates is dV=4πr2dr. Thus,
M=∫r0kr⋅4πr2dr=4πk∫r0rdr
Evaluating the integral:
M=4πk(r22)r0=2πkr2
3. Calculating the Gravitational Field (Acceleration):
The gravitational field g (which is equal to the acceleration a of the test particle) at distance r is given by:
g=GMr2
Substituting M:
g=G(2πkr2)r2=2πGk
Thus, for r≤R, the acceleration a is constant:
a=2πGk
4. Finding the Mass Outside Radius R:
For r>R, the total mass M1 of the sphere can be found by integrating from 0 to R:
M1=∫R0kr⋅4πr2dr=2πkR2
5. Calculating the Gravitational Field for r>R:
The gravitational field for r>R is:
g=GM1r2=G(2πkR2)r2
Thus, for r>R:
a=2πGkR2r2
This shows that the acceleration decreases with the square of the distance r.
6. Graphing the Acceleration:
- For r<R, the acceleration a is constant.
- For r>R, the acceleration a decreases as 1r2.
Conclusion:
The correct qualitative graph of acceleration a as a function of distance r will show a constant value for r<R and a decreasing curve for r>R.
The mass density is given by:
ρ(r)=krfor r≤R
ρ(r)=0for r>R
This indicates that the mass density decreases as we move away from the center of the sphere until we reach the radius R.
To find the total mass M within a radius r (where r≤R), we need to integrate the density over the volume:
M=∫r0ρ(r)dV
The volume element in spherical coordinates is dV=4πr2dr. Thus,
M=∫r0kr⋅4πr2dr=4πk∫r0rdr
Evaluating the integral:
M=4πk(r22)r0=2πkr2
The gravitational field g (which is equal to the acceleration a of the test particle) at distance r is given by:
g=GMr2
Substituting M:
g=G(2πkr2)r2=2πGk
Thus, for r≤R, the acceleration a is constant:
a=2πGk
For r>R, the total mass M1 of the sphere can be found by integrating from 0 to R:
M1=∫R0kr⋅4πr2dr=2πkR2
The gravitational field for r>R is:
g=GM1r2=G(2πkR2)r2
Thus, for r>R:
a=2πGkR2r2
This shows that the acceleration decreases with the square of the distance r.
- For r<R, the acceleration a is constant.
- For r>R, the acceleration a decreases as 1r2.
The correct qualitative graph of acceleration a as a function of distance r will show a constant value for r<R and a decreasing curve for r>R.
Similar Questions
Knowledge Check
Let there be a spherical symmetric charge density varying as p(r)=p0rR upto r = R and ρ(r)=0 for r>R, where r is the distance from the origin. The electric field at on a distance r(r<R) from the origin is given by -
Aρ0r24ε0RBρ0r4ε0RCρ0r4ε0RDρ0r2ε0RA spherically symmetric gravitational system of particles has a mass densityρ={ρ0forr<R0forr>R whereρ0 is a constant. A test mass can undergo circular motion under the influence of the gravitational field of particles. Its speed v as a function of distahce r(0<r<OO) form the centre of the system is represented by
A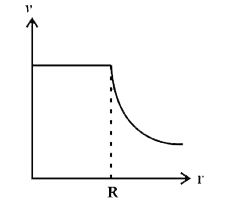 B
B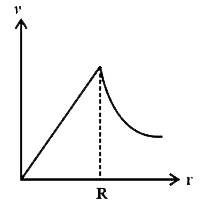 C
C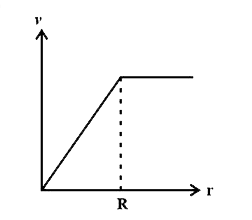 D
D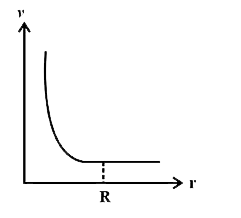
The potential energy function of a particle is given by U(r)=A2r2−B3r, where A and B are constant and r is the radial distance from the centre of the force. Choose the correct option (s)
AThe equilibrium distance will be r0=2ABBThe equilibrium distance will be r0=3ABCIf the total energy of the particle is B26A, then its radial velocity will vaishh ate r03, where r0 is the equilibrium distanceDIf the total energy of the particle is B26A, then its radial velocity will vanish at r02,where r0 is the equilibrium distance.
The density inside a solid sphere of radius a is given by ρ=ρ0r, where ρ0 is the density ast the surface and r denotes the distance from the centre. Find the graittional field due to this sphere at a distance 2a from its centre.
View SolutionThe density inside a solid sphere of radius a is given by ρ=ρ0(1−ra), where ρ0 is the density at the surface and r denotes the distance from the centre. Find the gravitational field due to this sphere at a distance 2a from its centre.
View SolutionThe mass density of a spherical galaxy varies as Kr over a large distance 'r' from its centre . In that region , a small star is in a circular orbit of radius R . Then the period of revolution , T depends on R as :
View SolutionLet there be a spherically symmetric charge distribution with charge density varying as ρ(r)=ρ(54−rR) upto r=R, and ρ(r)=0 for r>R, where r is the distance from the origin. The electric field at a distance r(rltR) from the origin is given by
View SolutionCharge density of a sphere of radius R is ρ=ρ0r where r is distance from centre of sphere.Total charge of sphere will be

View Solution
