A body of mass 2 kg is attached to another body of mass 1 kg with a massless rod. If 2 kg mass is at m, and 1 kg mass at m, find the centre of mass of that system.
To find the center of mass of the system consisting of two bodies with given masses and position vectors, we can follow these steps:
1. Identify the masses and their position vectors:
- Mass m1=2kg at position vector r1=(2^i+3^j)m
- Mass m2=1kg at position vector r2=(1^i+2^j)m
2. Use the formula for the center of mass (CM):
RCM=m1r1+m2r2m1+m2
3. Calculate the total mass:
m1+m2=2kg+1kg=3kg
4. Calculate the numerator (weighted position vectors):
- For m1:
m1r1=2kg⋅(2^i+3^j)=(4^i+6^j)kg m
- For m2:
m2r2=1kg⋅(1^i+2^j)=(1^i+2^j)kg m
5. Add the weighted position vectors:
m1r1+m2r2=(4^i+6^j)+(1^i+2^j)=(5^i+8^j)kg m
6. Divide by the total mass to find the center of mass:
RCM=(5^i+8^j)3=(53^i+83^j)m
Final Result:
The center of mass of the system is:
RCM=53^i+83^jm
---
- Mass m1=2kg at position vector r1=(2^i+3^j)m
- Mass m2=1kg at position vector r2=(1^i+2^j)m
RCM=m1r1+m2r2m1+m2
m1+m2=2kg+1kg=3kg
- For m1:
m1r1=2kg⋅(2^i+3^j)=(4^i+6^j)kg m
- For m2:
m2r2=1kg⋅(1^i+2^j)=(1^i+2^j)kg m
m1r1+m2r2=(4^i+6^j)+(1^i+2^j)=(5^i+8^j)kg m
RCM=(5^i+8^j)3=(53^i+83^j)m
The center of mass of the system is:
RCM=53^i+83^jm
Similar Questions
A body of mass 4 kg is attached to another body of mass 2 kg with a massless rod. If the 4 kg mass is at (2i + 5j)m and 2 kg mass is at (4i + 2j)m, the centre of mass of the system is at (in m)
View SolutionA rigid body consists of a 3kg mass connected to a 2kg mass by a massless rod. The 3kg mass is located at →r1=(2ˆi+5ˆj)m and the 2kg mass at →r2=(4ˆi+2ˆj)m. Find the length of rod and the coordinates of the centre of mass.
View Solution
Knowledge Check
Centre of mass of three particles of masses 1kg,2kgand3kg lies at the point (1,2,3) and centre of mass of another system of particles 3kgand2kg lies at the point (−1,3,−2). Where should we put a particle of mass 5kg so that the centre of mass of entire system lies at the centre of mass of first system ?
A(0, 0, 0)B(1, 3, 2)C(-1, 2, 3)D(3, 1, 8)
A man of mass m=2kg is standing on a platform of mass M=5kg, then at any instant.
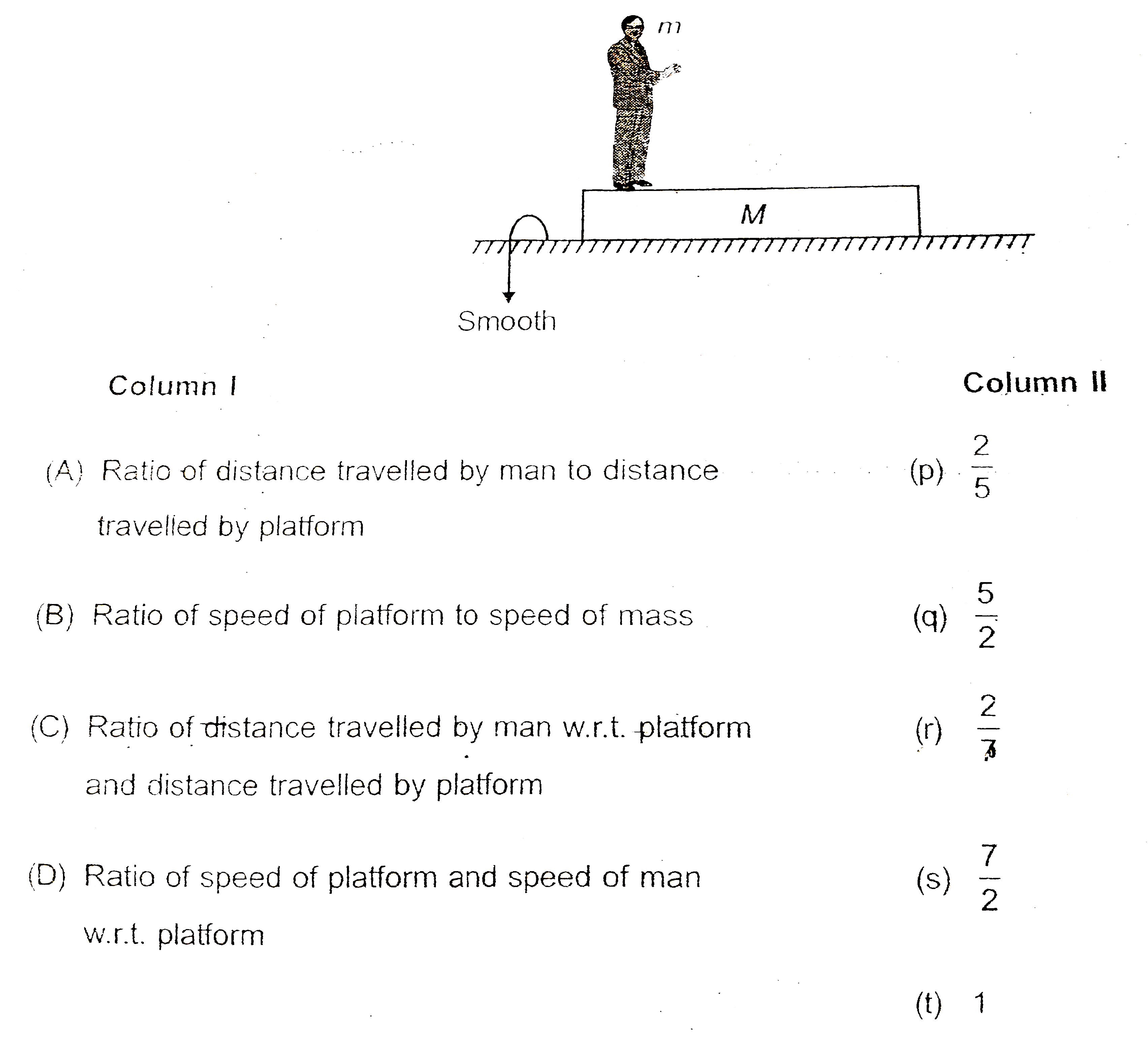
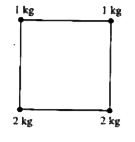
View SolutionFour point masses 1 kg, 1 kg, 2 kg and 2 kg are placed at the corners of a square of side a m as shown in Fig. Find the centre of mass of the system.
View SolutionA body A of mass 4 kg is dropped from a height of 100 m. Another body B of mass 2 kg is dropped from a height of 50 m at the same time. Then :
View SolutionTwo bodies of masses 1 kg and 3 kg are lying in xy plane at (0, 0) and (2, -1) respectively. What are the coordinates of the centre of mass ?
View SolutionConsider a system of two particles having masses 2kg and 5 kg the particle of mass 2 kg is pushed towards the centre of mass of particles through a distance 5 m,by what distance would particle of mass 5kg move so as to keep the centre of mass of particles at the original position?
View SolutionThree point masses of 1kg, 2kg and 3kg lie at (0,0), (1,2), (3,−1) respectively. Calculate the coordinates of the centre of mass of the system.
View SolutionThree point masses of 1kg, 2kg and 3kg lie at (0,0), (1,2), (3,−1) respectively. Calculate the coordinates of the centre of mass of the system.
View Solution