Three point masses of 1kg, 2kg and 3kg lie at (0,0), (1,2), (3,−1) respectively. Calculate the coordinates of the centre of mass of the system.
To calculate the coordinates of the center of mass of a system of point masses, we can use the following formulas:
1. Formula for the x-coordinate of the center of mass (X_COM):
XCOM=M1X1+M2X2+M3X3M1+M2+M3
2. Formula for the y-coordinate of the center of mass (Y_COM):
YCOM=M1Y1+M2Y2+M3Y3M1+M2+M3
Given Data:
- Masses:
- M1=1kg at (X1,Y1)=(0,0)
- M2=2kg at (X2,Y2)=(1,2)
- M3=3kg at (X3,Y3)=(3,−1)
Step 1: Calculate the total mass
Mtotal=M1+M2+M3=1+2+3=6kg
Step 2: Calculate the x-coordinate of the center of mass (X_COM)
XCOM=M1X1+M2X2+M3X3Mtotal
Substituting the values:
XCOM=(1×0)+(2×1)+(3×3)6
Calculating the numerator:
=0+2+96=116
Step 3: Calculate the y-coordinate of the center of mass (Y_COM)
YCOM=M1Y1+M2Y2+M3Y3Mtotal
Substituting the values:
YCOM=(1×0)+(2×2)+(3×−1)6
Calculating the numerator:
=0+4−36=16
Final Result
The coordinates of the center of mass are:
(116,16)
XCOM=M1X1+M2X2+M3X3M1+M2+M3
YCOM=M1Y1+M2Y2+M3Y3M1+M2+M3
- Masses:
- M1=1kg at (X1,Y1)=(0,0)
- M2=2kg at (X2,Y2)=(1,2)
- M3=3kg at (X3,Y3)=(3,−1)
Mtotal=M1+M2+M3=1+2+3=6kg
XCOM=M1X1+M2X2+M3X3Mtotal
Substituting the values:
XCOM=(1×0)+(2×1)+(3×3)6
Calculating the numerator:
=0+2+96=116
YCOM=M1Y1+M2Y2+M3Y3Mtotal
Substituting the values:
YCOM=(1×0)+(2×2)+(3×−1)6
Calculating the numerator:
=0+4−36=16
The coordinates of the center of mass are:
(116,16)
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBook:AAKASH INSTITUTE ENGLISHChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONExercise:Assignment (Section - J) Aakash Challengers Questions
Explore 13 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBook:AAKASH INSTITUTE ENGLISHChapter:SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSExercise:Assignment (Section-D (Assertion and reason))
Explore 5 Videos
- TEST 1Book:AAKASH INSTITUTE ENGLISHChapter:TEST 1Exercise:EXERCISE
Explore 21 Videos
Similar Questions
Two bodies of masses 1 kg and 3 kg are lying in xy plane at (0, 0) and (2, -1) respectively. What are the coordinates of the centre of mass ?
View SolutionTwo bodies of masses 1 kg and 2 kg are located at (1,2) and (-1,3), respectively. Calculate the coordinates of center of mass.
View SolutionTwo bodies of masses 1kg and 2kg are lying in xy plane at (-1,2) and (2,4) respectively. What are the coordinates of the center of mass?
View SolutionTwo bodies of masses 1kg and 3kg are lying in xy plane at (0,0) and (2,−1) respectively. What are the coordinates of the centre of mass ?
Hint. xcm=m1x1+m2x2m1+x2, ycm=m1y1+m2y2m1+m2
View SolutionThree point masses of 1 kg, 2kg and 3 kg lie at (0, 0), (1, 2), (3, -1), respectively. Calculate the coordinates of the centre of mass of the system.
View SolutionTwo particles of mass 1kg and 2kg are moving along the same line with speeds 2m/s and 4m/s respectively. Calculate the speed of the centre of mass of the system if both the particles are moving in the same direction.
View SolutionTwo bodies of masses 0.5 kg and 1 kg are lying in the X-Y plane at points (-1, 2) and (3, 4) respectively. Locate the centre of mass of the system.
View SolutionFour point masses 1 kg, 1 kg, 2 kg and 2 kg are placed at the corners of a square of side a m as shown in Fig. Find the centre of mass of the system.
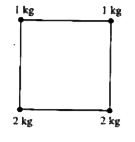
View SolutionFour particles of mass 5,3,2,4kg are at the points (1,6),(−1,5),(2,−3),(−1,−4) . Find the coordinates of their centre of mass.
View SolutionThree particles of masses 1.0 kg 2.0 kg and 3.0 kg are placed at the corners A,B and C respectively of an equilateral triangle ABC of edge 1m. Locate the centre of mass of the system.
View Solution