Three particle each of 1 kg mass are placed at corners of a right angled triangle AOB, 'O' being the origin of coordinate system (OA and OB along the x-direction and +ve y-direction). If OA = OB = 1m, the position vector of centre of mass (in metres) is
ˆi+ˆj3
ˆi−ˆj3
2(ˆi+ˆj)3
ˆi−ˆj
The correct Answer is:A
To find the position vector of the center of mass of three particles each of mass 1 kg placed at the corners of a right-angled triangle AOB, we can follow these steps:
Step 1: Define the Coordinates of the Points
- The origin O is at (0, 0).
- Point A is at (1, 0) since it lies 1 meter along the x-axis.
- Point B is at (0, 1) since it lies 1 meter along the y-axis.
Step 2: Identify the Masses
- Each particle has a mass of 1 kg.
- Therefore, we have:
- Mass at O (m1) = 1 kg at coordinates (0, 0)
- Mass at A (m2) = 1 kg at coordinates (1, 0)
- Mass at B (m3) = 1 kg at coordinates (0, 1)
Step 3: Calculate the Total Mass
- Total mass (M) = m1 + m2 + m3 = 1 kg + 1 kg + 1 kg = 3 kg.
Step 4: Calculate the Coordinates of the Center of Mass
The coordinates of the center of mass (CM) can be calculated using the formula:
CM=(m1x1+m2x2+m3x3M,m1y1+m2y2+m3y3M)
Substituting the values:
- For the x-coordinate:
xCM=(1⋅0)+(1⋅1)+(1⋅0)3=0+1+03=13
- For the y-coordinate:
yCM=(1⋅0)+(1⋅0)+(1⋅1)3=0+0+13=13
Step 5: Write the Position Vector of the Center of Mass
The position vector of the center of mass is given by:
→rCM=xCM^i+yCM^j=13^i+13^j
Final Answer
Thus, the position vector of the center of mass is:
→rCM=13^i+13^j (in metres)
---
- The origin O is at (0, 0).
- Point A is at (1, 0) since it lies 1 meter along the x-axis.
- Point B is at (0, 1) since it lies 1 meter along the y-axis.
- Each particle has a mass of 1 kg.
- Therefore, we have:
- Mass at O (m1) = 1 kg at coordinates (0, 0)
- Mass at A (m2) = 1 kg at coordinates (1, 0)
- Mass at B (m3) = 1 kg at coordinates (0, 1)
- Total mass (M) = m1 + m2 + m3 = 1 kg + 1 kg + 1 kg = 3 kg.
The coordinates of the center of mass (CM) can be calculated using the formula:
- For the x-coordinate:
xCM=(1⋅0)+(1⋅1)+(1⋅0)3=0+1+03=13
yCM=(1⋅0)+(1⋅0)+(1⋅1)3=0+0+13=13
The position vector of the center of mass is given by:
→rCM=xCM^i+yCM^j=13^i+13^j
Thus, the position vector of the center of mass is:
→rCM=13^i+13^j (in metres)
Similar Questions
Four particles, each of mass 1kg, are placed at the corners of a square OABC of side 1m. 'O' is at the origin of the coordinate system. OA and OC are aligned along positive x-axis and positive y-axis respectively. The position vector of the centre of mass is (in 'm')
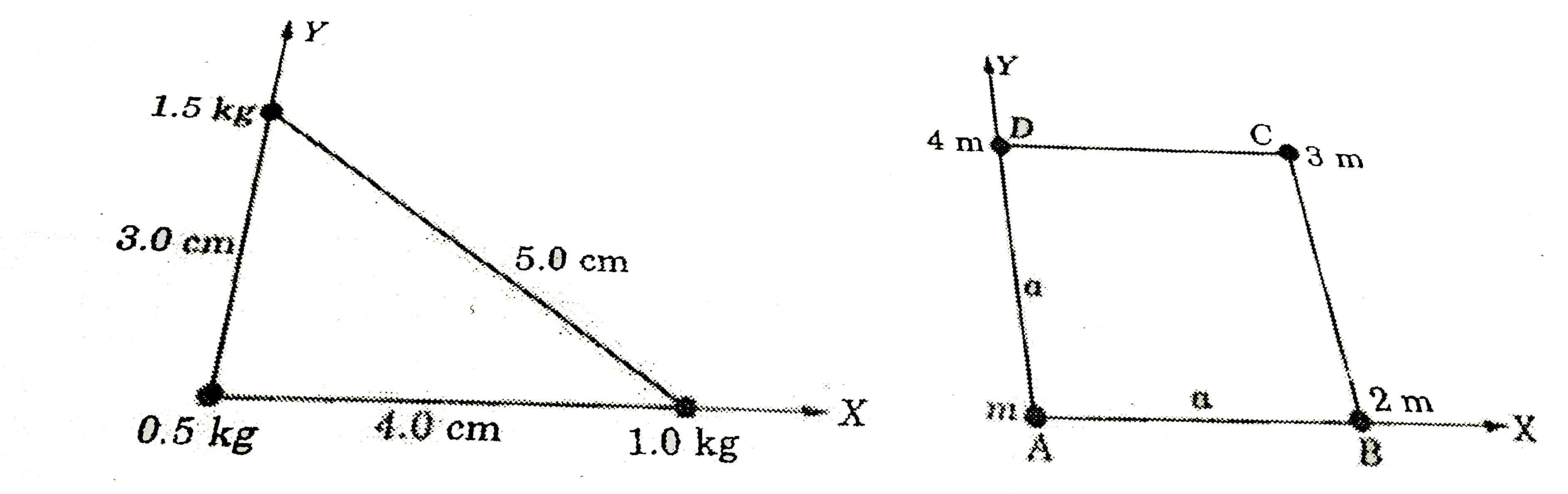
View SolutionThree particles of masses 0.50 kg, 1.0 kg and are placed at the corners of a right angle triangle, as shown in fig. Locate the centre of mass of the system.
View SolutionThree charges +q,−q,and+2q are placed at the verticles of a right angled triangle (isoceles triangle) as shown. The net electrostatic energy of the configuration is :

View SolutionThree point particles of masses 1.0 kg, 1.5 kg and 2.5 kg are placed at three corners of a right angle triangle as shown in figure. The centre of mass of the system is at a point :
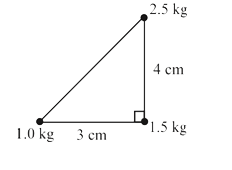
View SolutionThree point particles of masses 1.0 kg, 1.5 kg and 2.5 kg are placed at three corners of a right angle triangle as shown in figure. The centre of mass of the system is at a point :

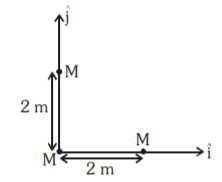
View SolutionThree identical spheres each of mass M are placed at corners of right angle triangle with mutually perpendicular sides equal to 2m. Taking point of intersection of two mutually perpendicular sides as origin find position vector center of mass
View SolutionThree particle of mass m each are placed at the three corners of an equilateral triangle of side a. Find the work which should be done on this system to increase the sides of the triangle to 2a.
View SolutionThree particle of mass m each are placed at the three corners of an equilateral triangle of side a. Find the work which should be done on this system to increase the sides of the triangle to 2a.
View SolutionThree particle of mass m each are placed at the three corners of an equilateral triangle of side a. Find the work which should be done on this system to increase the sides of the triangle to 2a.
View SolutionThree identical spheres of mass M each are placed at the corners of an equilateral triangle of side 2 m. Taking one of the corners as the origin, the position vector of the centre of mass is
View Solution