A conducting rod MN moves with a speed v parallel to a long straight wire which carries a constant current i, as shown in Fig. The length of the rod is normal to the wire. Find the emf induced in the total length of the rod. State which end will be at a lower potential.
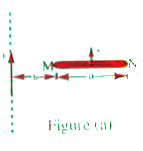
The magnetic field induction due to current i is different at different sections of the rod, because they are at different distances from the wire. Let us, first of all, subdivide the entire length of the conductor MN into elementary sections. Consider a section (shown shaded in the figure (b)) of thickness dx at a distance x from the wire. As all the three, v, B and (dX) are mutually normally to each other, so the emf induced in it is de = Bvdx.
(from N to M by Fleming.s right hand rule)

For the rest of sections, the induced emf is in the same sense, (i.e, from N to M)
∴ Total emf induced in the conductor is
e=∫de=∫b+abBvdx
Substituting for B=μ0i2πx , the above equation gets changed to
e=∫b+abμ0ivdx2πx
e=μ0iv2π[lnx]b−ab or e=μ0iv2πln(1+alb)
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-IA
58 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-IB
18 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-II)
26 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -II
22 Videos
Similar Questions
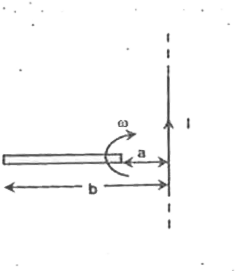
A copper rod moves with a constant angular velocity ω about a long straight wire carrying a current I. If the ends of the rod from the wire are at distances a and b, then the e.m.f induced in the rod is
View SolutionA rod of length l is kept parallel to a long wire carrying constant current i . It is moving away from the wire with a velocity v. Find the emf induced in the wire when its distance from the long wire is x.
View SolutionA thin rod, carrying current i2 is placed near a long straight wire carrying current i1 in the plane of rod as shown in figure. The motion of rod is
View SolutionA rod of length l is kept parallel to a long wire carrying constant current i . It is moving away from the wire with a velocity v. Find the emf induced in the wire when its distance in the wire when its distance from the long wire is x.
View SolutionShow a conduction loop placed near a long, straight wire carrying current i as shown. If the current increases continuously, find the direction of the induced current in the loop.

View SolutionA rod of length l is placed perpendicular to a long wire carrying current i. The rod is moved parallel to the wire with a velocity v. Find the emf induced in the rod, if its nearest end is at a distance a from the wire.

View SolutionA rod of length l is placed perpendicular to a long wire carrying current i. The rod is moved parallel to the wire with a velocity v. Find the emf induced in the rod, if its nearest end is at a distance a from the wire.

View Solution
The end B of the rod AB which makes angle θ with the floor is being pulled with a constant velocity vv as shown. The length of the rod is l.
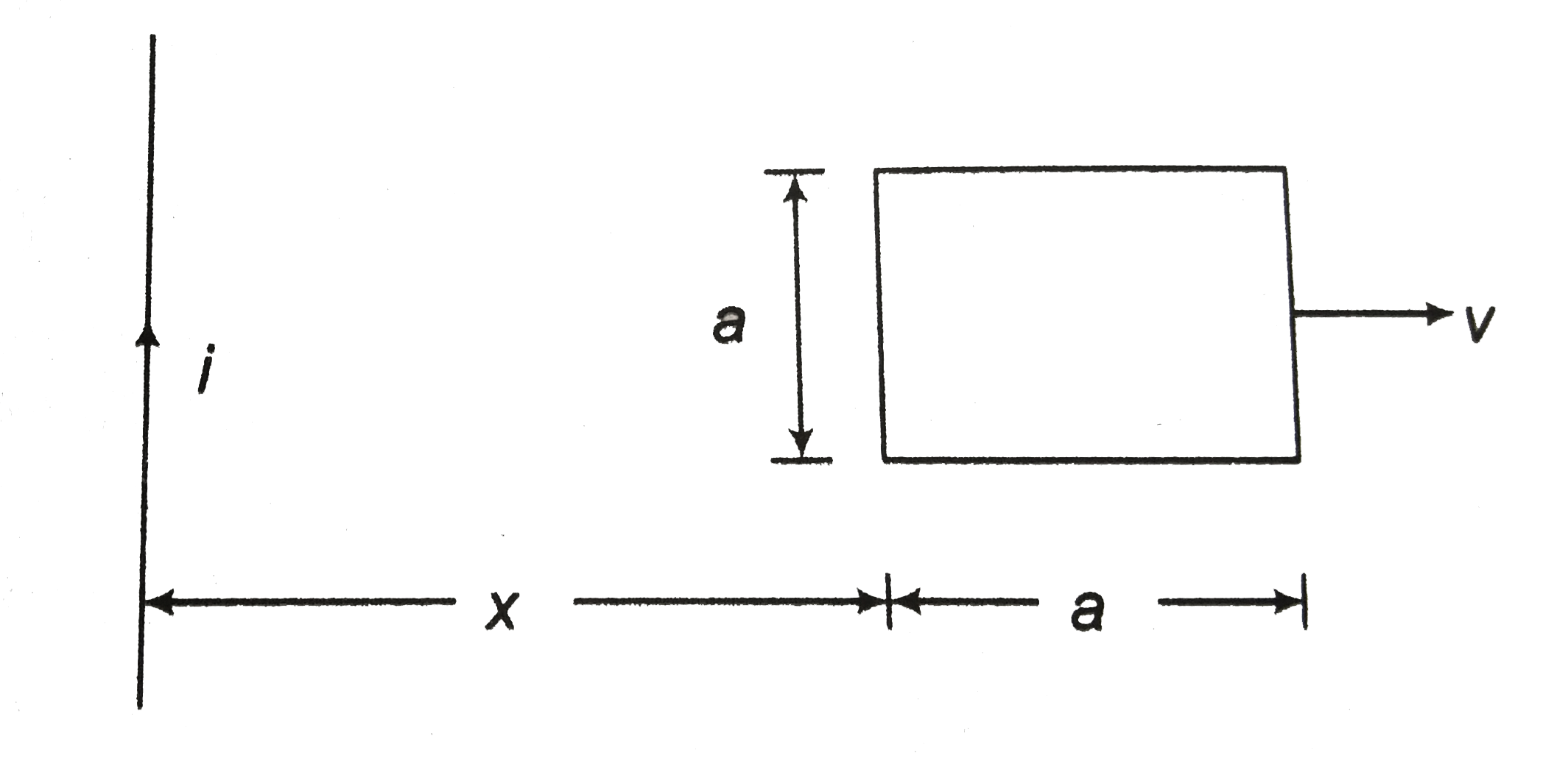
View SolutionA square frame with side a and a long straight wire carrying a current i are located in the same plane as m shown in figure. The fram translates to the right with a constant velocity v. Find the emf induced in the frame as a function of distance x.
View SolutionThree long, straight and parallel wires are arranged as shown in Fig. The forces experienced by 10 cm length of wire Q is

View Solution
