The balancing lengths of potentiometer wire are 800 cm and 600cm when two cells of emf's E1andE2 are connected in the secondary circuit first in series and then terminals of one cell is reversed,E1E2is equal to
1/11
14/11
7/1
4/3
The correct Answer is:C
To solve the problem, we need to find the ratio of the EMFs E1E2 based on the balancing lengths of a potentiometer wire when two cells are connected in different configurations.
1. Understanding the Problem:
We have two cells with EMFs E1 and E2. The balancing lengths of the potentiometer wire are given as 800 cm when the cells are connected in series and 600 cm when the terminals of one cell are reversed.
2. Setting Up the Equations:
- When the cells are connected in series, the total EMF is E1+E2. The balancing length is proportional to the EMF, so we can write:
E1+E2=k⋅800(1)
where k is a constant of proportionality.
- When one terminal of E2 is reversed, the effective EMF becomes E1−E2. The balancing length in this case is:
E1−E2=k⋅600(2)
3. Dividing the Equations:
We can divide equation (1) by equation (2):
E1+E2E1−E2=800600=43
4. Cross-Multiplying:
Cross-multiplying gives us:
3(E1+E2)=4(E1−E2)
5. Expanding and Rearranging:
Expanding both sides:
3E1+3E2=4E1−4E2
Rearranging gives:
3E2+4E2=4E1−3E1
Simplifying this results in:
7E2=E1
6. Finding the Ratio:
Thus, we can express the ratio of E1 to E2:
E1E2=71
Final Answer:
The ratio E1E2 is 7:1.
We have two cells with EMFs E1 and E2. The balancing lengths of the potentiometer wire are given as 800 cm when the cells are connected in series and 600 cm when the terminals of one cell are reversed.
- When the cells are connected in series, the total EMF is E1+E2. The balancing length is proportional to the EMF, so we can write:
E1+E2=k⋅800(1)
where k is a constant of proportionality.
- When one terminal of E2 is reversed, the effective EMF becomes E1−E2. The balancing length in this case is:
E1−E2=k⋅600(2)
We can divide equation (1) by equation (2):
E1+E2E1−E2=800600=43
Cross-multiplying gives us:
3(E1+E2)=4(E1−E2)
Expanding both sides:
3E1+3E2=4E1−4E2
Rearranging gives:
3E2+4E2=4E1−3E1
Simplifying this results in:
7E2=E1
Thus, we can express the ratio of E1 to E2:
E1E2=71
The ratio E1E2 is 7:1.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - PRACTICE SHEET (EXERCISE - V LEVEL-II (ADVANCED) (Straight Objective Type Questions))4videos
CURRENT ELECTRICITY
- BOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - PRACTICE SHEET (EXERCISE - V LEVEL-II (ADVANCED) (More than One correct answer Type Questions))3videos
CURRENT ELECTRICITY
- BOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - PRACTICE SHEET (EXERCISE - IV LEVEL-II (ADVANCED) (Integer Type Questions))2videos
CURRENT ELECTRICITY
- BOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - PROBLEMS (LEVEL-II)27videos
CURRENT ELECTRICITY
- BOOK - AAKASH SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - PRACTICE EXERCISEX42videos
DUAL NATURE OF RADIATION AND MATTER
Similar Questions
Two cells of emf E1 and E2 are connected to two resistors R1andR2 as shown. If E2 is short circuited then current through R1andR2 are
 View Solution
View SolutionTow cells of e.m.f E1 and E2 are joined in series and the balancing length of the potentiometer wire is 625 cm. If the terminals of E1 are reversed , the balancing length obtained is 125 cm. Given E2>E1,the ratio E1:E2 willbe
View SolutionThe length of the potentiometer wire is 600 cm and a current of 40 mA is flowing in it. When a cell of emf 2 V and internal resistance 10Ω is balanced on this potentiometer the balance length is found to be 500 cm. The resistance of potentiometer wire will be
View SolutionThe length of a potentiometer wire is 600cm and it carries a current of 40mA. For a cell of emf 2V and internal resistance 10Ω, the null point is found to be ast 500cm. On connecting a voltmeter acros the cell, the balancing length is decreased by 10cm
The voltmeter reading will beView SolutionTwo batteries of e.m.f. E1 and E2 and internal resistance r1 and r2 are connected in parallel. Determine their equivelent e.m.f.
View SolutionIn a potentiometer experiment two cells of e.m.f. E1 and E2 are used in series and in conjunction and the balancing length is found to be 58 cm of the wire. If the polarity of E2 is reversed, then the balancing length becomes 29 cm . The ratio E1E2 of the e.m.f. of the two cells is
View SolutionTwo primary cells of emfs E1 and E2 are connected to the potentiometer wire AB as shown in the figure . If the balancing lengths for the two combinations of the cells are 250 cm and 400 cm , find the ratio of E1 and E2 .
 View Solution
View SolutionAB is a potentiometer wire of length 100cm. When a cell E2 is connected across AC, where AC=75cm, no current flows from E2. The internal resistance of the cell E1 is negligible.
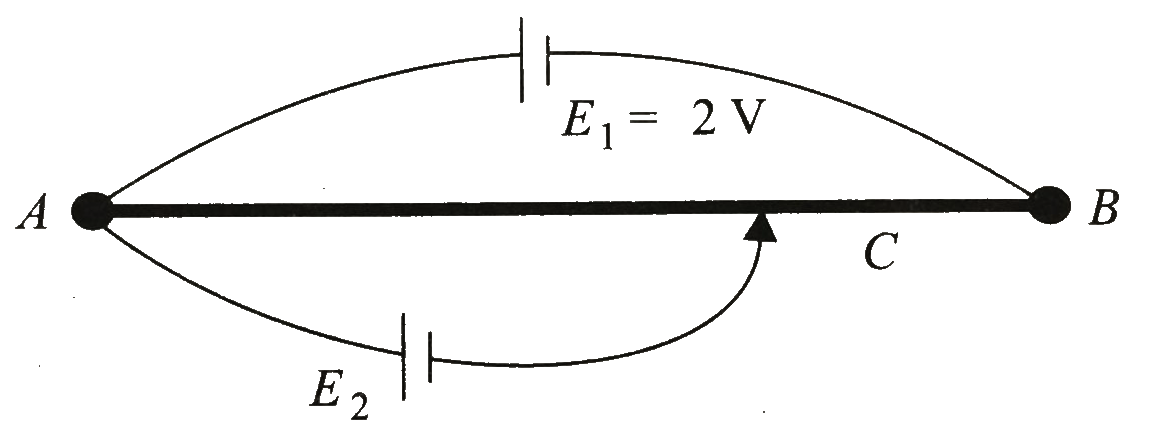
Find emf of the cell E2.View SolutionThe length of potentiometer wire is 200 cm and the emf of standard cell is primary circuit is E volts. It is employed to a battery of emf 0.4 v the balance point is obtained at l = 40 cm from positive end, the E of the battery is (cell in primary is ideal and series resistance is zone
View SolutionA cell of e.mf. E and internal resistance r is connected in series with an external resistance nr. Then, the ratio of the terminal potential difference to E.M.F.is
View Solution
