A metallic conductor at 10∘C connected in the left gap of Meter Bridge given balancing length 40cm. When the conductor is at 60∘C, the balancing point shifts by__cm, (temperature coefficient of resistance of the material of the wire is (1/220)/∘C)
4.8
8.7
15
7
The correct Answer is:A
To solve the problem step by step, we will use the concepts of the meter bridge and the temperature dependence of resistance.
Step 1: Understand the meter bridge principle
The meter bridge is based on the principle of Wheatstone bridge. It states that when the bridge is balanced, the ratio of the lengths of the bridge is equal to the ratio of the resistances.
Step 2: Set up the initial conditions
Let:
- R be the resistance of the metallic conductor at 10∘C.
- The balancing length l1=40cm.
- The length on the other side of the meter bridge 100−l1=60cm.
Using the meter bridge formula:
xR=l1100−l1
where x is the resistance on the left side of the bridge.
Step 3: Calculate the initial resistance
From the balancing condition:
xR=4060
Cross-multiplying gives:
x=R⋅4060=R⋅23
Step 4: Determine the resistance at 60∘C
The resistance of the conductor changes with temperature according to the formula:
Rt=R0(1+αΔT)
where:
- R0 is the resistance at 10∘C.
- α=1220∘C−1 (temperature coefficient).
- ΔT=60−10=50∘C.
Substituting the values:
R60=R0(1+1220⋅50)=R0(1+50220)=R0(1+522)=R0(2722)
Step 5: Set up the new balancing condition
Let the new balancing length at 60∘C be l2. The new balancing condition is:
xR60=l2100−l2
Step 6: Substitute the new resistance
Using the expression for R60:
xR0⋅2722=l2100−l2
Substituting x=R0⋅23:
R0⋅23R0⋅2722=l2100−l2
This simplifies to:
23⋅2227=l2100−l2
Step 7: Solve for l2
Cross-multiplying gives:
2(100−l2)=3l2⋅2227
Expanding and simplifying:
200−2l2=6627l2
Combining like terms:
200=2l2+6627l2
Finding a common denominator (27):
200=(54+66)l227
200=120l227
Thus:
l2=200⋅27120=5400120=45cm
Step 8: Calculate the shift in balancing point
The shift in the balancing point is:
Δl=l2−l1=45cm−40cm=5cm
Final Answer
The balancing point shifts by 5 cm.
The meter bridge is based on the principle of Wheatstone bridge. It states that when the bridge is balanced, the ratio of the lengths of the bridge is equal to the ratio of the resistances.
Let:
- R be the resistance of the metallic conductor at 10∘C.
- The balancing length l1=40cm.
- The length on the other side of the meter bridge 100−l1=60cm.
xR=l1100−l1
where x is the resistance on the left side of the bridge.
From the balancing condition:
xR=4060
Cross-multiplying gives:
x=R⋅4060=R⋅23
The resistance of the conductor changes with temperature according to the formula:
Rt=R0(1+αΔT)
where:
- R0 is the resistance at 10∘C.
- α=1220∘C−1 (temperature coefficient).
- ΔT=60−10=50∘C.
R60=R0(1+1220⋅50)=R0(1+50220)=R0(1+522)=R0(2722)
Let the new balancing length at 60∘C be l2. The new balancing condition is:
xR60=l2100−l2
Using the expression for R60:
xR0⋅2722=l2100−l2
Substituting x=R0⋅23:
R0⋅23R0⋅2722=l2100−l2
This simplifies to:
23⋅2227=l2100−l2
Cross-multiplying gives:
2(100−l2)=3l2⋅2227
Expanding and simplifying:
200−2l2=6627l2
Combining like terms:
200=2l2+6627l2
Finding a common denominator (27):
200=(54+66)l227
200=120l227
Thus:
l2=200⋅27120=5400120=45cm
The shift in the balancing point is:
Δl=l2−l1=45cm−40cm=5cm
The balancing point shifts by 5 cm.
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:AAKASH SERIESChapter:CURRENT ELECTRICITYExercise:LECTURE SHEET (EXERCISE-IV LEVEL- II (ADVANCED) (Straight Objective Type Questions))
Explore 2 Videos
- CURRENT ELECTRICITYBook:AAKASH SERIESChapter:CURRENT ELECTRICITYExercise:LECTURE SHEET (EXERCISE-IV LEVEL- II (ADVANCED) (Linked Comprehension Type Questions))
Explore 3 Videos
- CURRENT ELECTRICITYBook:AAKASH SERIESChapter:CURRENT ELECTRICITYExercise:LECTURE SHEET (EXERCISE-III LEVEL- II (ADVANCED) (Linked Comprehension Type Questions)
Explore 2 Videos
- CURRENT ELECTRICITYBook:AAKASH SERIESChapter:CURRENT ELECTRICITYExercise:PROBLEMS (LEVEL-II)
Explore 27 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:AAKASH SERIESChapter:DUAL NATURE OF RADIATION AND MATTERExercise:PRACTICE EXERCISEX
Explore 42 Videos
Similar Questions
If the resistance of a conductor is 5Ω at 50∘C and 7Ω at 100∘C then the mean temperature coefficient of resistance of the material is
View SolutionIn meter bridge when P is kept in left gap, Q is kept in right gap, the balancing length is 40cm. If Q is shunted by 10Ω, the balance point shifts by 10cm. Resistance Q is
View Solution
Knowledge Check
When a metal conductor connected to left gap of a meter bridge is heated, the balancing point
Ashifts towards rightBshifts towards leftCremains unchangedDremains at zeroA wire connected in the left gap of a meter bridge balance a 10Ω resistance in the right gap to a point, which divides the bridge wire in the ratio 3:2. If the length of the wire is 1m. The length of one ohm wire is
A0.057mB0.067mC0.37mD0.134m
A metallic wire has a resistance of 3.0Ω at 0∘C and 4.8Ω at 150∘C. Find the temperature coefficient of resistance of its material.
View SolutionResistance in the two gaps of a meter bridge are 10ohm and 30ohm respectively. If the resistances are interchanged he balance point shifts by
View SolutionA 6Ω resistance is connected in the left gap of a meter bridge. In the second gap 3Ω and 6Ω are joined in parallel. The balance point of the bridge is at _______
View SolutionA student performs meter bridge experiment to determine specific resistance of a conducting wire of length 10cm and diameter 1mm. When a standard 6Ω resistance is connected on left gap and the given conducting wire is connected on the right gap, the balance points obtained for 60cm length of the meter bridge wire. The specific resistance in Ω−m for material of the given wire is:
View SolutionWhen a conducting wire is connected in the left gap and known resistance in the right gap, the balance length is 75cm. If the wire is cut into 3 equal parts and one part isconnected in the left gap, the balance length
View SolutionIn a meter bridge circuit as shown in the figure, the bridge is balanced when AJ=20 cm. On interchanging P and Q the balance length shifts by
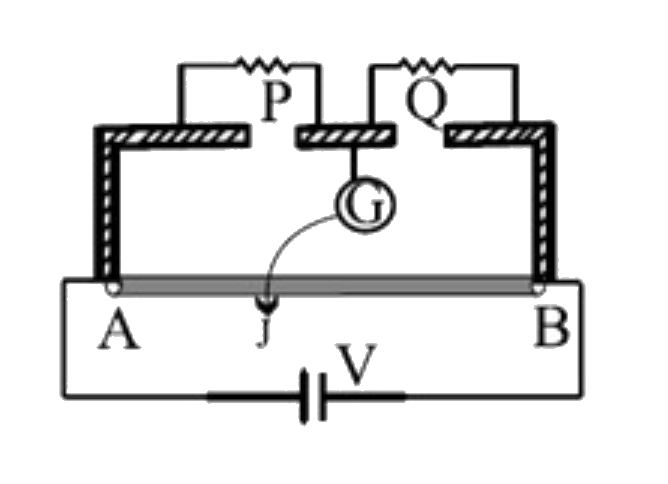
View Solution

