A sperical capacitor composed of two concentric metal spheres one having a radius twice as large as the other. The region in which the energy is stored has a volume of
14c3π2ε30
116c3π2ε20
1384c3π2ε30
7c3384π2ε20
The correct Answer is:D
To solve the problem of finding the volume of the region in which energy is stored in a spherical capacitor composed of two concentric metal spheres, we can follow these steps:
1. Define the Radii of the Spheres:
Let the radius of the inner sphere be R1=R and the radius of the outer sphere be R2=2R.
2. Identify the Volume of the Region:
The energy is stored in the space between the two spheres. The volume V of this region can be calculated as the difference between the volume of the outer sphere and the volume of the inner sphere.
3. Calculate the Volume of the Outer Sphere:
The volume V2 of the outer sphere (radius R2) is given by the formula:
V2=43πR32=43π(2R)3=43π(8R3)=323πR3
4. Calculate the Volume of the Inner Sphere:
The volume V1 of the inner sphere (radius R1) is given by the formula:
V1=43πR31=43πR3
5. Find the Volume of the Region Between the Spheres:
The volume of the region where energy is stored is:
V=V2−V1=323πR3−43πR3=32πR3−4πR33=28πR33
6. Final Expression for the Volume:
Thus, the volume of the region in which the energy is stored in the spherical capacitor is:
V=283πR3
Let the radius of the inner sphere be R1=R and the radius of the outer sphere be R2=2R.
The energy is stored in the space between the two spheres. The volume V of this region can be calculated as the difference between the volume of the outer sphere and the volume of the inner sphere.
The volume V2 of the outer sphere (radius R2) is given by the formula:
V2=43πR32=43π(2R)3=43π(8R3)=323πR3
The volume V1 of the inner sphere (radius R1) is given by the formula:
V1=43πR31=43πR3
The volume of the region where energy is stored is:
V=V2−V1=323πR3−43πR3=32πR3−4πR33=28πR33
Thus, the volume of the region in which the energy is stored in the spherical capacitor is:
V=283πR3
Topper's Solved these Questions
- CAPACITORS Book:AAKASH SERIESChapter:CAPACITORS Exercise:PRACTICE SHEET (ADVANCED) (Linked Comprehension Type Questions Passage)
Explore 1 Video
- CAPACITORS Book:AAKASH SERIESChapter:CAPACITORS Exercise:PRACTICE SHEET (ADVANCED) (Integer Type Questions)
Explore 2 Videos
- CAPACITORS Book:AAKASH SERIESChapter:CAPACITORS Exercise:ADDITIONAL PRACTICE EXERCISE (LEVEL - II LECTURE SHEET (ADVANCED))(Integer Type Questions )
Explore 3 Videos
- ATOMSBook:AAKASH SERIESChapter:ATOMSExercise:PRACTICE EXERCISE
Explore 21 Videos
- COMMUNICATION SYSTEM Book:AAKASH SERIESChapter:COMMUNICATION SYSTEM Exercise:LECTURE SHEET (LEVEL - I) (MAIN) (EXERCISE - IV) (Straight Objective & More than one Correct Answer Type Questions)
Explore 20 Videos
Similar Questions
There are two metallic spheres of same radii but one is solid and the other is hollow, then
View SolutionA spherical capacitor has the inner sphere of radius 2cm and the outerone of 4cm. If the inner sphere is earthed and the outer one is charged with a charge of 2μC and isolated. Calculate ltbr> (a) the potential to which the outer sphere is raised.
(b) the charge retained on the outer surface of the outer sphere.
View Solution
Knowledge Check
A metallic sphere of radius 18 cm has been given a charge of 5×10−6C. The energy of the charged conductor is
A0.2JB0.6JC1.2JD2.4J
A spherical capacitor has an inner sphere of radius 12 cm and an outer sphere of radius 13 cm. The outer sphere is earthed and the inner sphere is given a charge of 2.5μC. The space between the concentric spheres is filled with a liquid of dielectric constant 32.
(a) Determine the capacitance of the capacitor. (b) What is the potential of the inner sphere ?
(c) Compare the capacitance of this capacitor with that of an isolated sphere of radius 12 cm.Explain why the later is much smaller ?
View SolutionA sherical capacitor has an inner sphere of radius 12cm and an outer spere of radius 13cm. The outer sphere is earthed, and the inner sphere is given a charge of 2.5μC. The space between the concentric spjheres is filled with a liquid of dielectric caonstant 32. Determine the potential of the inner sphere.
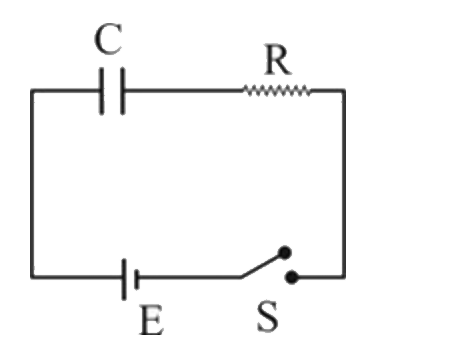
View SolutionThe capacitor shown in the figure is initially unchanged, the battery is ideal. The switch S is closed at time t= 0, then the time after which the energy stored in the capacitor becomes one - fourth of the energy stored in it in steady - state is :
View SolutionA capacitor of capacitance C1 is charged to a potential V1 while another capacitor of capacitance C2 is charged to a potential difference V2 . The capacitors are now disconnected from their respective charging batteries and connected in parallel to each other .
(a) Find the total energy stored in the two capacitors before they are connected.
(b) Find the total energy stored in the parallel combination of the two capacitors.
(c ) Explain the reason for the difference of energy in parallel combination in comparison to the total energy before they are connected.
View SolutionTwo identical conduction spheres, one having an initial charge +Q and the other initially uncharged, are brought into contact.
(a) What is the new charge on each sphere?
(b) While the spheres are in contact, a positively chaged rod is moved close to one sphere, causing a redistribution of hte charges on the two spheres so the charge on hte sphere closest to the rod has a charge-Q. What is the charge to the other sphere?
View SolutionA hollow metallic sphere of radius 20cm surrounds a concentric metallic sphere of radius 5cm. The space between the two sphere is filled with a nonmetallic material. The inner and outer sphere are maintained at 50∘C and 10∘C respectively and it is found that 100J of heat passes from the inner sphere to the outer sphere per second. Find the thermal conductivity of the material between the sphere.
View SolutionOf the bulbs in a house, one glows brighter than the other, which of the two has a large resistance.
View Solution
