A parallel plate capacitor with air as dielectric is charged to a potential .v. using a battery . Removing the battery. The charged capacitor is then connected across an identical uncharged parallel plate capacitor filled with was of dielectric constant k. The common potential of both the capacitor is
V volts
kV volts
(k+1) V volts
Vk+1 volts
The correct Answer is:D
To solve the problem step by step, let's break it down clearly:
Step 1: Understand the Initial Conditions
We have a parallel plate capacitor (let's call it Capacitor 1) charged to a potential V with air as the dielectric. The dielectric constant of air is k=1. The capacitance of this capacitor is C1=C.
Step 2: Calculate Initial Charge
The charge Q on Capacitor 1 when it is charged to potential V can be calculated using the formula:
Q=C1⋅V=C⋅V
Step 3: Remove the Battery
After charging, the battery is removed, and the charge Q remains on Capacitor 1 since it is isolated.
Step 4: Connect to the Second Capacitor
Now, we connect Capacitor 1 (charged) to an identical uncharged capacitor (let's call it Capacitor 2) which has a dielectric material with dielectric constant K. The capacitance of Capacitor 2 is:
C2=K⋅C
Step 5: Calculate Total Capacitance
When the two capacitors are connected in parallel, the total capacitance Ctotal becomes:
Ctotal=C1+C2=C+K⋅C=C(1+K)
Step 6: Apply Charge Conservation
Since charge is conserved, the initial charge on Capacitor 1 is equal to the total charge on the combined system:
Q=C⋅V=Ctotal⋅Vcommon
Where Vcommon is the common potential across both capacitors after they are connected.
Step 7: Substitute for Ctotal
Substituting Ctotal into the equation gives:
C⋅V=C(1+K)⋅Vcommon
Step 8: Solve for Vcommon
Now, we can solve for Vcommon:
Vcommon=C⋅VC(1+K)=V1+K
Final Answer
Thus, the common potential across both capacitors after they are connected is:
Vcommon=V1+K
---
We have a parallel plate capacitor (let's call it Capacitor 1) charged to a potential V with air as the dielectric. The dielectric constant of air is k=1. The capacitance of this capacitor is C1=C.
The charge Q on Capacitor 1 when it is charged to potential V can be calculated using the formula:
Q=C1⋅V=C⋅V
After charging, the battery is removed, and the charge Q remains on Capacitor 1 since it is isolated.
Now, we connect Capacitor 1 (charged) to an identical uncharged capacitor (let's call it Capacitor 2) which has a dielectric material with dielectric constant K. The capacitance of Capacitor 2 is:
C2=K⋅C
When the two capacitors are connected in parallel, the total capacitance Ctotal becomes:
Ctotal=C1+C2=C+K⋅C=C(1+K)
Since charge is conserved, the initial charge on Capacitor 1 is equal to the total charge on the combined system:
Q=C⋅V=Ctotal⋅Vcommon
Where Vcommon is the common potential across both capacitors after they are connected.
Substituting Ctotal into the equation gives:
C⋅V=C(1+K)⋅Vcommon
Now, we can solve for Vcommon:
Vcommon=C⋅VC(1+K)=V1+K
Thus, the common potential across both capacitors after they are connected is:
Vcommon=V1+K
Topper's Solved these Questions
- CAPACITORS Book:AAKASH SERIESChapter:CAPACITORS Exercise:PRACTICE SHEET (EXERCISE - IV) (LEVEL - II (ADVANCED) (Straight Objective Type Questions )
Explore 5 Videos
- CAPACITORS Book:AAKASH SERIESChapter:CAPACITORS Exercise:PRACTICE SHEET (EXERCISE - IV) (LEVEL - II (ADVANCED) (More than one correct answer Type Questions)
Explore 4 Videos
- CAPACITORS Book:AAKASH SERIESChapter:CAPACITORS Exercise:PRACTICE SHEET (EXERCISE - III) (LEVEL - II (ADVANCED)) (Integer Type Questions)
Explore 1 Video
- ATOMSBook:AAKASH SERIESChapter:ATOMSExercise:PRACTICE EXERCISE
Explore 21 Videos
- COMMUNICATION SYSTEM Book:AAKASH SERIESChapter:COMMUNICATION SYSTEM Exercise:LECTURE SHEET (LEVEL - I) (MAIN) (EXERCISE - IV) (Straight Objective & More than one Correct Answer Type Questions)
Explore 20 Videos
Similar Questions
Parallel Plate Capacitors with and without Dielectric
View SolutionTwo parallel plate capacitors of capacitances C and 2C are connected in parallel and charged to a potential difference V. The battery is then disconnected and the region between the plates of the capacitor C is completely filled with a material of dielectric constant K. The potential differences across the capacitors now becomes...........
View SolutionA parallel plate capacitor of capacitance C is charged to a potential V and then disconnected with the battery. If separation between the plates is decreased by 50% and the space between the plates is filled with a dielectric slab of dielectric constant K=10. then
View SolutionHalf of the space between the plates of a parallel plate capacitor is filled with dielectric material of constant K. Then which of the plots are possible?
View SolutionThe terminals of a battery of emf V are connected to the two plates of a parallel plate capacitor. If the space between the plates of the capacitor is filled with an insulator of dielectric constant K, then :
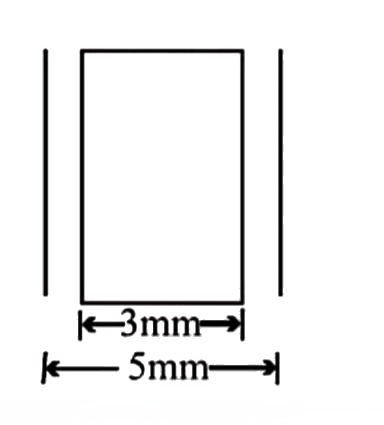
View SolutionSeparation between the plates of parallel plate capacitor is 5 mm. this capacitor, having air as the dielectric medium between the plates, is charged to a potential difference 25 V using a battery. The battery is then disconnected and a dielectric slab of thickness 3mm and dielectric constant K=10 is placed between the plates as shown. potential difference between the plates after the dielectric slab has been introduced is-
View SolutionIn a parallel plate capacitor of capacitor 1μF two plates are given charges 2μC and 4μC the potential difference between the plates of the capacitor is
_2019_CBT2_E01_002_Q01.png)
View SolutionTwo identical parallel plate air capacitors are connected in series to a battery of emf V. If one of the capacitor is completely filled with dielectric material of constant K, then potential difference of the other capacitor will become
View SolutionA parallel plate capacitor has two layers of dielectrics as shown in figure. This capacitor is connected across a battery, then the ratio of potential difference across the dielectric layers is

View SolutionAnswer the following:
(a) Describe briefly the process of transferring charge between the two plates of a parallel plate capacitor when connected to a battery. Derive an expression for the energy stored in a capacitor.
(b) A parallel plate capacitor is connected to a battery of potential difference V. It is disconnected from battery and then connected to another uncharged capacitor of the same capacitance. Calculate the ratio of the energy stored in the combination to the initial energy on the single capacitor.
View Solution