A copper rod of length 2m is rotated with a speed of 10 rps, in a uniform magnetic field of T tesla about a pivot at one end. The magnetic field is perperndicular to the plane of rotation. Find the emf induced across its ends
To find the electromotive force (emf) induced across the ends of a rotating copper rod in a magnetic field, we can follow these steps:
Step 1: Identify the given values
- Length of the copper rod (L) = 2 m
- Speed of rotation (N) = 10 revolutions per second (rps)
- Magnetic field (B) = T tesla (unknown value)
Step 2: Convert the speed of rotation to angular velocity
The angular velocity (ω) in radians per second can be calculated using the formula:
ω=2πN
Substituting the value of N:
ω=2π×10=20πrad/s
Step 3: Use the formula for induced emf
The formula for the induced emf (E) in a rotating rod is given by:
E=12BωL2
where:
- B = magnetic field strength in tesla
- ω = angular velocity in rad/s
- L = length of the rod in meters
Step 4: Substitute the values into the formula
Now, substituting the known values into the formula:
E=12×B×(20π)×(22)
Calculating L2:
L2=22=4
Now substituting this back into the equation:
E=12×B×(20π)×4
E=40πB
Step 5: Calculate the numerical value of emf
Using the approximate value of π≈3.14:
E=40×3.14×B=125.6Bvolts
Final Result
The induced emf across the ends of the copper rod is:
E=125.6Bvolts
- Length of the copper rod (L) = 2 m
- Speed of rotation (N) = 10 revolutions per second (rps)
- Magnetic field (B) = T tesla (unknown value)
The angular velocity (ω) in radians per second can be calculated using the formula:
ω=2πN
Substituting the value of N:
ω=2π×10=20πrad/s
The formula for the induced emf (E) in a rotating rod is given by:
E=12BωL2
where:
- B = magnetic field strength in tesla
- ω = angular velocity in rad/s
- L = length of the rod in meters
Now, substituting the known values into the formula:
E=12×B×(20π)×(22)
Calculating L2:
L2=22=4
Now substituting this back into the equation:
E=12×B×(20π)×4
E=40πB
Using the approximate value of π≈3.14:
E=40×3.14×B=125.6Bvolts
The induced emf across the ends of the copper rod is:
E=125.6Bvolts
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-IA
58 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-IB
18 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-II)
26 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -II
22 Videos
Similar Questions
A copper rod of length 2m is rotated with a speed of 10 rps, in a uniform magnetic field of 1 tesla about a pivot at one end. The magnetic field is perpendicular to the plane of rotation. Find the emf induced across its ends
View SolutionA rod of length 20 cm is rotating with angular speed of 100 rps in a magnetic field of strength 0.5 T about it’s one end . What is the potential difference betweet two ends of the rod :
View Solution
Knowledge Check
A copper rod of length L rotates with an angular with an angular speed 'ω' in a uniform magnetic field B. find the emf developed between the two ends of the rod. The field in perpendicular to the motion of the rod.
ABωl2B12Bωl2C2Bωl2D14Bωl2
A conductor of length 0.1m is moving with a velocity of 4m/ s in a uniform magnetic field of 2T as shown in the figure. Find the emf induced ?
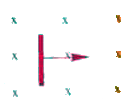
View SolutionA conductor of length 0.1m is moving with a velocity of 4m/s in a uniform magnetic field of 2T as shown in the figure. Find the emf induced ?
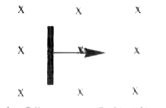
View SolutionA copper disc of radius 1 m is rotated about its natural axis with an angular velocity 2 rad/sec in a uniform magnetic field of 5 tesla with its plane perpendicular to the field. Find the emf induced between the centre of the disc and its rim.
View SolutionA copper disc of radius 0.1 m is rotated about its natural axis with 10 rps in a uniform magnetic field of 0.1 T with its plane perpendicular to the field, The emf induced across the radius of the disc is
View SolutionA copper rod of length l is rotated about one end perpendicular to the uniform magnetic field B with constant angular velocity ω . The induced e.m.f. between its two ends is
View SolutionA conducting rod OA of length l is rotated about its end O with an angular velocity ω in a uniform magnetic field directed perpendicualr to the rotation. Find the emf induced in the rod, between it's ends.
View SolutionA rectangular coil of 300 turns has an average area of average area of 25cm×10cm the cooil rotates with a speed of 50cps in a uniform magnetic field of strength 4×10−2T about an axis perpendicular of the field. The peak value of the induced e.m.f. is (in volt)
View Solution
