Four forces are acting on a particle. One forces of magnitude 3N is directed upward, another is directed 37∘ East of North having magnitude 5N third is directed in South-West direction is of magnitude 4√2N and fourth force is √5nN. If the partice in equilibrium. Find the value of n.
The correct Answer is:0
To solve the problem of finding the value of n such that the particle is in equilibrium under the influence of four forces, we will follow these steps:
Step 1: Identify the Forces
1. Force 1: F1=3N (upward)
2. Force 2: F2=5N (directed 37∘ East of North)
3. Force 3: F3=4√2N (South-West direction)
4. Force 4: F4=√5nN (unknown direction)
Step 2: Resolve Forces into Components
- Force 2:
- F2x=5sin(37∘) (East component)
- F2y=5cos(37∘) (North component)
Using the trigonometric values:
- sin(37∘)=35
- cos(37∘)=45
Calculating the components:
- F2x=5⋅35=3N
- F2y=5⋅45=4N
- Force 3 (South-West direction):
- The angle is 45∘ from both South and West.
- F3x=−4√2⋅1√2=−4N (West component)
- F3y=−4√2⋅1√2=−4N (South component)
Step 3: Sum the Forces in Each Direction
- Net Force in the x-direction:
Fnetx=F2x+F3x=3−4=−1N
- Net Force in the y-direction:
Fnety=F1+F2y+F3y=3+4−4=3N
Step 4: Calculate the Resultant Force
The resultant force R can be calculated using the Pythagorean theorem:
R=√(Fnetx)2+(Fnety)2=√(−1)2+(3)2=√1+9=√10N
Step 5: Set the Fourth Force Equal to the Resultant Force
For the particle to be in equilibrium, the fourth force must balance the resultant force:
F4=√5n=√10
Step 6: Solve for n
n=√10√5=√105=√2
Conclusion
The value of n is √2.
---
1. Force 1: F1=3N (upward)
2. Force 2: F2=5N (directed 37∘ East of North)
3. Force 3: F3=4√2N (South-West direction)
4. Force 4: F4=√5nN (unknown direction)
- Force 2:
- F2x=5sin(37∘) (East component)
- F2y=5cos(37∘) (North component)
- sin(37∘)=35
- cos(37∘)=45
- F2x=5⋅35=3N
- F2y=5⋅45=4N
- The angle is 45∘ from both South and West.
- F3x=−4√2⋅1√2=−4N (West component)
- F3y=−4√2⋅1√2=−4N (South component)
- Net Force in the x-direction:
Fnetx=F2x+F3x=3−4=−1N
Fnety=F1+F2y+F3y=3+4−4=3N
The resultant force R can be calculated using the Pythagorean theorem:
R=√(Fnetx)2+(Fnety)2=√(−1)2+(3)2=√1+9=√10N
For the particle to be in equilibrium, the fourth force must balance the resultant force:
F4=√5n=√10
n=√10√5=√105=√2
The value of n is √2.
Similar Questions
Four forces are acting on particle.One forces of magnitude 3N is directed upward .another directed 37 east of north having magnitude 5N Third is directed in south west direction is magnitude 4root2N and fourth force is root5n N ,If the particle in equilibrium ,Find The value of n
View SolutionTwo forces of magnitudes 3N and 4N are acted on a body. The ratio of magnitude of minimum and maximum resultant force on the body is
View Solution
Knowledge Check
Two forces each of magnitude 2N, act at an angle of 60∘. The magnitude of the resultant force
A√1.1 NewtonB√4 NewtonC√12 NewtonD√14.9 Newton
A block is applied two forces of magnitude 5N each. One force is acting towards East and the other acting along 60∘ North of East. The resultant of the two forces (in N) is of magnitude :-
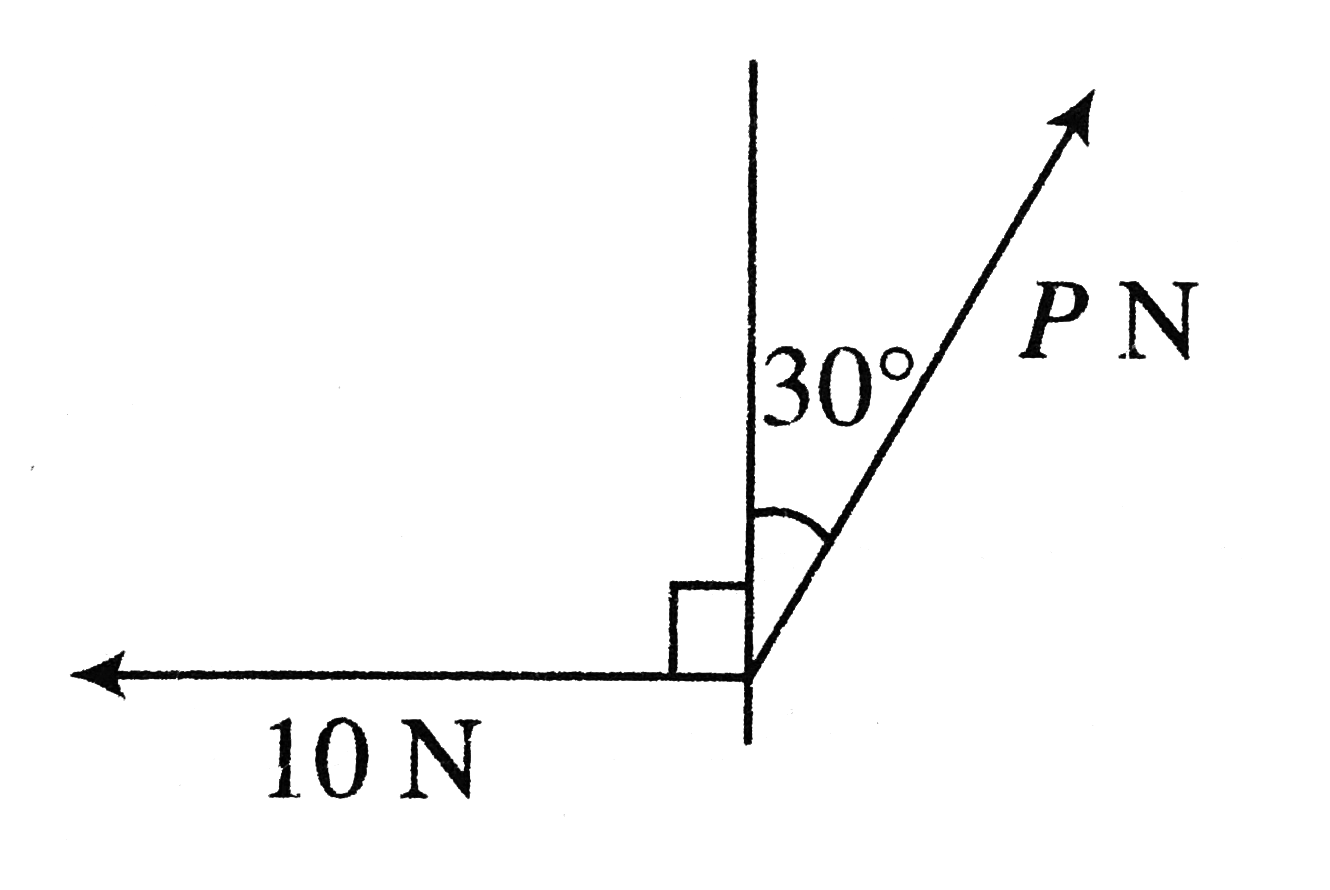
View SolutionTwo horizontal forces of magnitudes of 10N and PN act on a particle. The force of magnitude 10N acts due west and the force of magnitude PN acts on a bearing of 30∘ east of north as shown in (figure) The resultant of these two force acts due north. Find the magnitude of the resultant.
View SolutionIf two forces each of magnitude 20N, are acting on a particle such that the first force (→E1) is acting along east direction and the second force (vercF2) is acting along the direction 60∘ north of west, then the magnitude of resultant force on particle is
View SolutionTwo forces of magnitudes 3N and 4 N act together on an object making an angle 60∘ with each other. Find the resultant force acting on the object.
View SolutionTwo perpendicular forces of magnitudes 10 N and 5 N act at a point. Find their resultant.
View SolutionTwo forces are such that the sum of their magnitudes is 18 N, the resultant is √228 when they are at 120∘. Then the magnitude of the forces are
View SolutionTwo forces, while acting on particle in opposite directions,have the resultant of 10N. If they act at right angles to each other, the resultant is found to be 50N. Find the two forces?
View Solution