A source and a detector move away from each other, each with a speed of 10 m/s with respect to ground with no wind. If the detector detects a frequency 1650 Hz of the sound coming from the source, what is the original frequency of the source? (speed of sound = 340 m/s
750 Hz
1750 Hz
2000 Hz
1800 Hz
The correct Answer is:B
To find the original frequency of the source when both the source and the detector are moving away from each other, we can use the Doppler effect formula for sound. Here’s a step-by-step solution:
Step 1: Identify the given values
- Apparent frequency detected by the observer (f') = 1650 Hz
- Speed of sound in air (v) = 340 m/s
- Speed of the source (v_s) = 10 m/s
- Speed of the observer (v_o) = 10 m/s
Step 2: Write the formula for apparent frequency
When both the source and the observer are moving away from each other, the formula for the apparent frequency (f') is given by:
f′=v−vov+vs⋅f
Where:
- f′ = apparent frequency
- f = original frequency of the source
- v = speed of sound
- vo = speed of the observer
- vs = speed of the source
Step 3: Rearrange the formula to solve for the original frequency (f)
To find the original frequency (f), we rearrange the formula:
f=f′⋅v+vsv−vo
Step 4: Substitute the known values into the formula
Now, we substitute the known values into the rearranged formula:
f=1650⋅340+10340−10
Step 5: Calculate the values in the equation
Calculate the numerator and denominator:
- Numerator: 340+10=350
- Denominator: 340−10=330
Now substitute these values back into the equation:
f=1650⋅350330
Step 6: Perform the multiplication and division
Now, calculate the value:
f=1650⋅350330=1650⋅1.060606≈1750 Hz
Step 7: Conclusion
Thus, the original frequency of the source is approximately 1750 Hz.
---
- Apparent frequency detected by the observer (f') = 1650 Hz
- Speed of sound in air (v) = 340 m/s
- Speed of the source (v_s) = 10 m/s
- Speed of the observer (v_o) = 10 m/s
When both the source and the observer are moving away from each other, the formula for the apparent frequency (f') is given by:
- f′ = apparent frequency
- f = original frequency of the source
- v = speed of sound
- vo = speed of the observer
- vs = speed of the source
To find the original frequency (f), we rearrange the formula:
Now, we substitute the known values into the rearranged formula:
Calculate the numerator and denominator:
- Denominator: 340−10=330
Now, calculate the value:
Thus, the original frequency of the source is approximately 1750 Hz.
Topper's Solved these Questions
- WAVESBOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-III (Wave Equations & Basics)
7 Videos
- WAVESBOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-III (Strings (Speed of travelling wave))
15 Videos
- WAVESBOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-II (Beats : )
20 Videos
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - PROBLEMS (LEVEL - II)
33 Videos
- WAVES OPTICSBOOK - AAKASH SERIESCHAPTER - WAVES OPTICSEXERCISE - EXERCISE -III (POLARISITION)
10 Videos
Similar Questions
A source and a detector move away from each other, each with a speed of 10ms−1 with respect to the ground with no wind. If the detector detects a frequency 1950 Hz of the sound coming from the source, what is the original frequency of the source? Speed of sound in air =340ms−1.
View SolutionTwo cars A and B are moving away from each other in opposite directions. Both the cars are moving with a speed of 20ms−1 with respect to the ground. If an observer in car A detects a frequency 2000 Hz of the sound coming from car B, what is the natural frequency of the sound source in car B? (Speed of sound in air =340ms−1)
View SolutionA siren emitting a sound of frequency 2000 Hz moves away from you towards a cliff at a speed of 8 m/s.
(a) What is the frequency of the sound you hear coming directly from the siren.
(b) What is the frequency of sound you hear reflected off the cliff. Speed of sound in air is 330ms.
View SolutionWhen both source and observer approach each other with a speed a equal to the half the speed of sound, then determine the percentage change in frequency of sound as detected by the listener.
View SolutionOn the same path, the source and observer are moving such a way that the distance between these two increases with the time. The speeds of source and observer are same and equal to 10ms−1 with respect to the ground while no wind in blowing. The apparent frequency received by observer is 1950Hz then the original frequency must be (the speed of sound in present medium is 340m/s
View SolutionA sound source moving with speed 50 m/s along x-axis and observer at rest on y-axis.If the frequency observed by observer when source crosses the origin is 96 Hz, then the original frequency of source is :(speed of sound is given medium is 200 m/s)
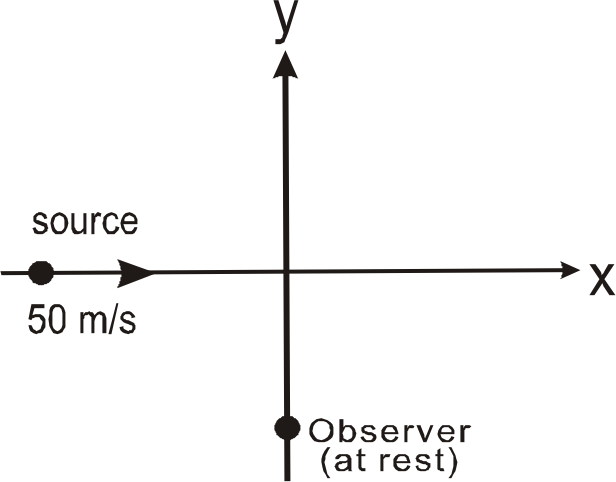
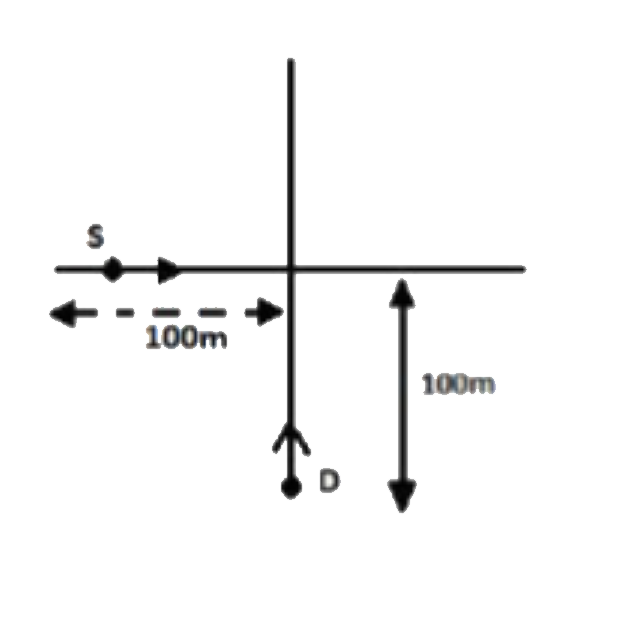
View SolutionThe figure shows the location of a source and detector at time t = 0. The source and detector are moving with velocities vs=5ˆims−1andvD=10ˆjms−1 respectively . The frequency of signals received by the detector at the moment when the source cros the origin is (the frequency of the source is 100 Hz . Velocity bof sound 330ms−1 .)
View SolutionA source of sound and an observer are approaching each other with the same speed, which is equal to (110) times the speed of sound. The apparent relative change in frequency of source is
View SolutionAn echo is returned in 3s. What is the distance of the reflecting surface from the source, given that the speed of sound is 342m/s.
View SolutionAn observer is moving towards a source with speed 15 m/s. The source is moving with speed 5 m/s in the same direction. Air is blowing with speed 10 m/s from observer to source. If frequency of sound emitted is 325 Hz then find frequency of sound heard by observer (velocity of sound in air = 330 m/s) in Hz .
View Solution
