Two wires of equal length and cross-section area suspended as shown in figure. Their Young's modulus are Y1 and Y2 respectively. The equavalent Young's modulus will be

F=F1+F2⇒Y(2A)el=Y1Ael+Y2Ael
2Yeq=Y1+Y2⇒Yeq=Y1+Y22
Similar Questions
Two wires of equal length and cross sectional area suspended as shown in
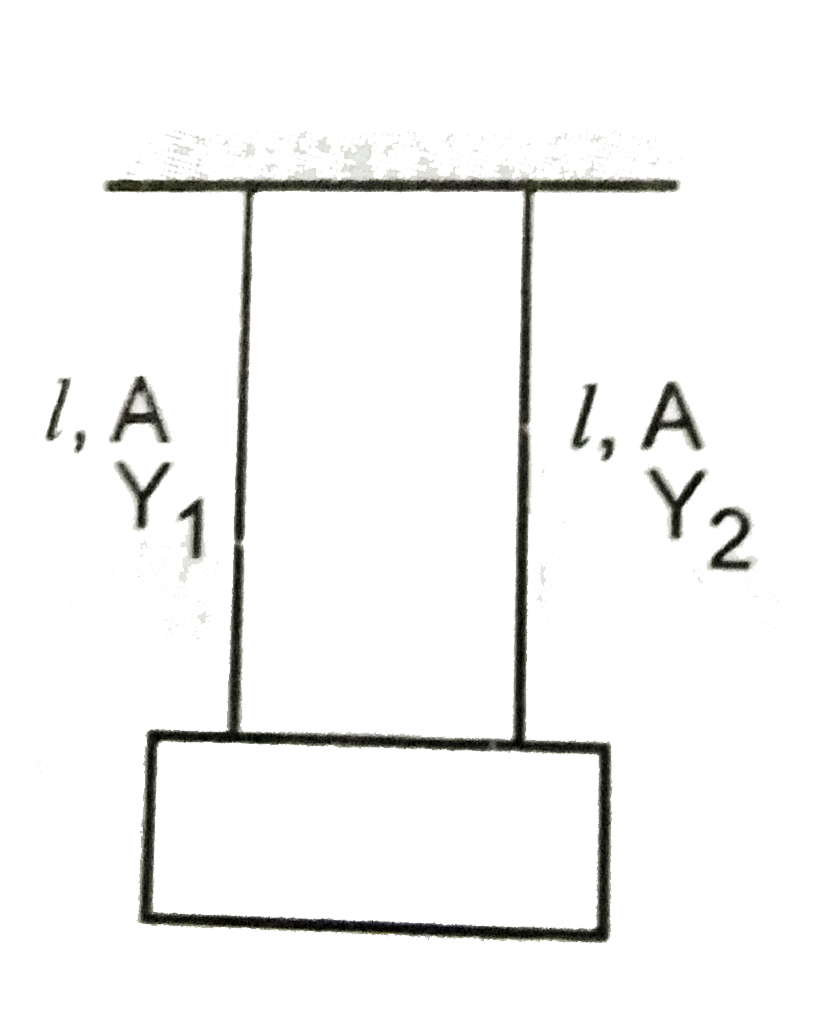
Their Young's modulii are Y1=2×1011 Pa and Y2=0.90×1011 Pa respectively. What will be the equivalent Young's modulus of combination?
View SolutionTwo wires of equal length and cross sectional area suspended as shown in

Their Young's modulii are Y1=2×1011 Pa and Y2=0.90×1011 Pa respectively. What will be the equivalent Young's modulus of combination?
View Solution
Knowledge Check
A wire of length L and cross-sectional area A is made of a material of Young's modulus Y. IF the wire is stretched by an amount x, the workdone is
AYAx22LBYAx2L2CYAx2LDYAx2L
Two wires have identical lengths and areas of cross-section are suspended by mass M. Their Young's modulus are in the ratio 2:5.
View SolutionA wire havinga length L and cross- sectional area A is suspended at one of its ends from a ceiling . Density and young's modulus of material of the wire are ρ and Y, respectively. Its strain energy due to its own weight is ρ2g2AL3αY. Find the vqalue of α
View SolutionA wire of length l and cross-sectional are A is suspended at one of its ends from a ceiling. What will be its strain energy due to its own weight, if the density and Young's modulus of the material of the wire be d and Y?
View SolutionA force F doubles the length of wire of cross-section a The Young modulus of wire is
View SolutionTwo steel rods and an aluminium rod of equal length l0 and equal cross- section are joined rigidly at their ends as shown in the figure below. All the rods are in a state of zero tension at 0∘C. Find the length of the system when the temperature is raised to θ. Coefficient of linear expansion of aluminium and steel are αa and αs respectively. Young's modulus of aluminium is Ya and of steel is Ys.
View SolutionThe Young's modulus of a wire is numerically equal
View SolutionThe Young's modulus of the material of a wire is equal ot the
View Solution