A smooth pulley A of mass M0 is lying on a frictionless table. A massless rope passes round the pulley and has masses M1 and M2 tied to its ends, the two portions of the string being perpendicular to the edge of the table so that the masses hang vertically. Find the acceleration of the pulley.
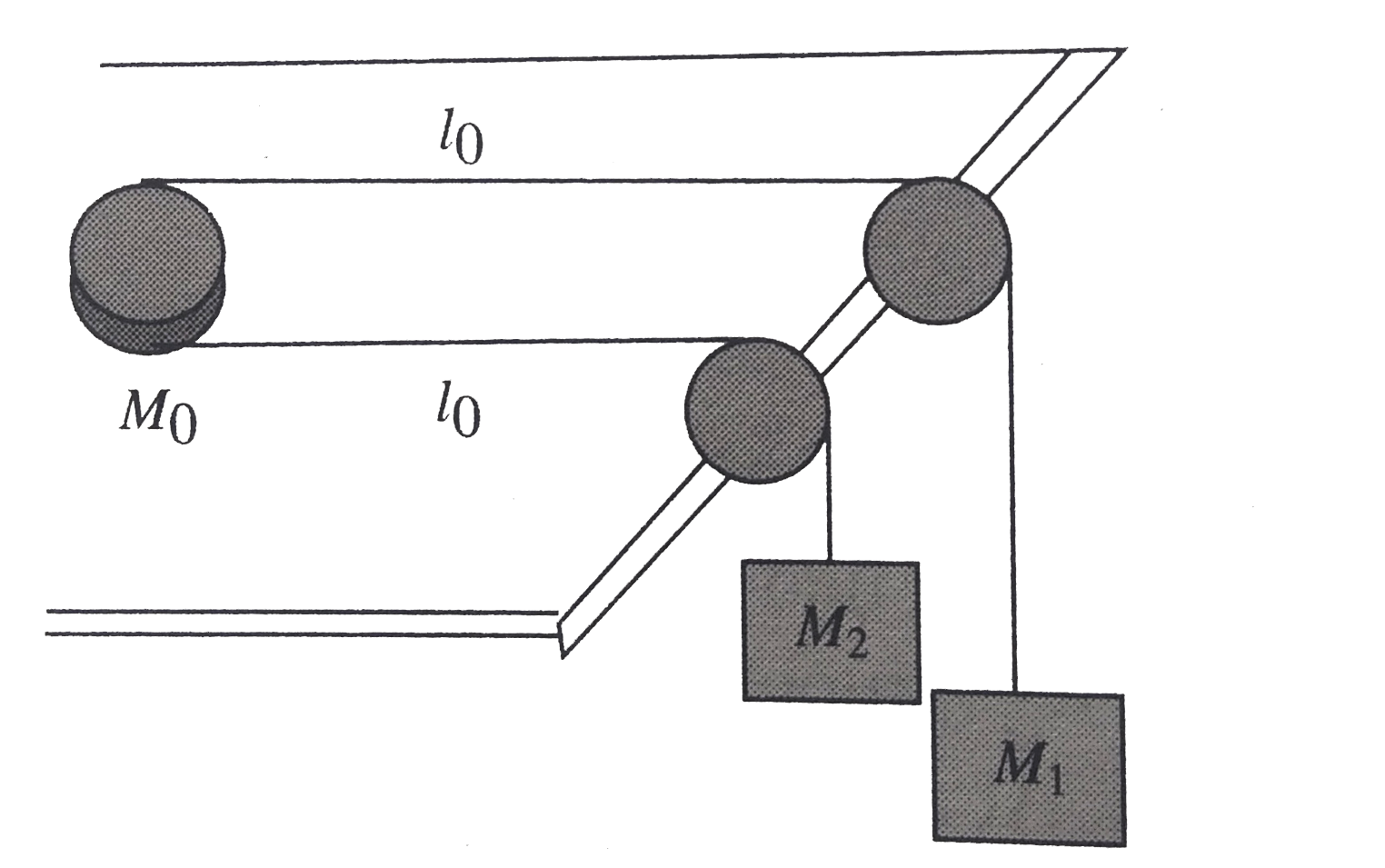
Let the length of portions of string on the table be l0,l1andl2 as shown in figure .
Let mass M0 move to the right by x on the table , M1 goes down by y1andM2 goes up by y2 .
Then l0 becomes (l0−x),l1 becomes (l1+y1)andl2 becomes (l2−y2).
As the length of string remains unchanged
2l0+l1+l2=2(l0−x)+l1+y1+l2−y2
or 2x=y1−y2
Diff. twice w.r. to t,
we get 2d2xdt2=d2y1dt2−d2y2dt2
If a0,a1anda2 are acceleration of

M0,M1andM2 respectively , then
2a0=a1−a2 ......... (1)
For motion of M0,2T=M0a0 ....... (2)
M1g−T=M1a1....... (3)
For motion of mass M2 ,
T−m2g=M2a2 .......... (4)
Substituting values of a0,a1anda2 from (2) , (3) and (4) in equation (1) , we get
2(2TM0)=(g−TM1)−(TM2−g),
4TM0=2g−T(1M1+1M2)i.e.,(4M0+1M1+1M2)T=2g
This gives T=2M0M1M2g4M1M2+M0(M1+M2)........ (5)
∴ Acceleration of puelly A from (2)
a0=2TM0=4M1M2g4M1M2+M0(M1+M2) ............ (6)
Similar Questions
Two bodies of masses 4 kg and 6 kg are tied to the ends of a massless string. The string passes over a frictionless pulley. The acceleration of the system is :
View SolutionA block of mass 20 kg is set into motion on a frictionless horizontal surface with the help of massless smooth pulley and rope as shown in the figure. Find the acceleration of the pulley
_PHY_E05_192_Q05.png)
View SolutionA pulley fixed to the ceiling carried a thread with bodies of masses m1 and m2 attached to its ends. The mases of the pulley and the thread are negligible and friction is absent. Find the acceleration of the centre of mass of this system.
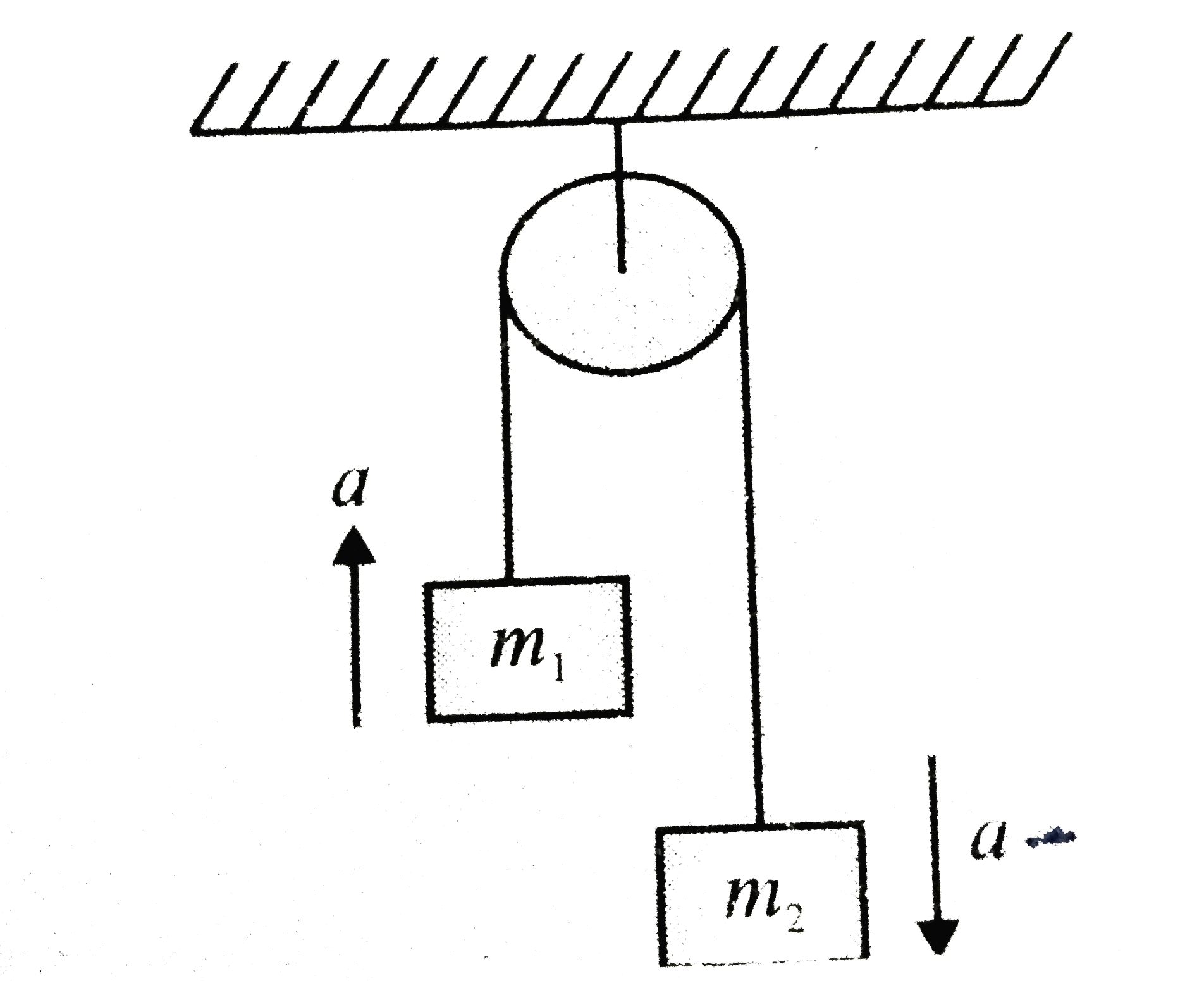
View SolutionWhat is the mechanical advantage of single fixed pulley:-

View SolutionIn the arrangement shown in fig. pulleys are smooth and massless. Threads are massless and inextensible. Find acceleration of mass m1.

View SolutionA block of mass of 20kg is set into motion on a frictionless horizontal surface with the help of massless smooth pulley and rope as shown in figure.Find the acceleration of the pulley
_PHY_E05_034_Q01.png) .jpg
.jpg
View SolutionTwo mass m1andm2 are attached to a flexible inextensible massless rope, which passes over a frictionless and massless pully. Find the accelerations of the masses and tension in the rope.

View SolutionIn the arrangement shown, the mass m will ascend with an acceleration ( Pulley and rope are massless)

View SolutionIn the arrangement shown, the mass m will ascend with an acceleration ( Pulley and rope are massless)

View SolutionA block of mass m1 rests on a horizontal table. A string tied to the block is passed on a frictionless pulley fixed at the end of the table and to the other end of string is hung another block of mass m2. The acceleration of the system is
View Solution
